”秒殺引き算”から文字指導へ
■ 同じ教材でも導入の在り方で,その後の展開が「天と地」の違いになる場合があります.学習者の心理をベースにした,Rさん(当時大学3年生)の印象深い文字活用の導入例を紹介します.
■ まずは動画①をご覧ください(Rさんの導入例を参考にしました).
■ 続いて動画②をご覧ください.
出だしで”ひきつける”,Rさん
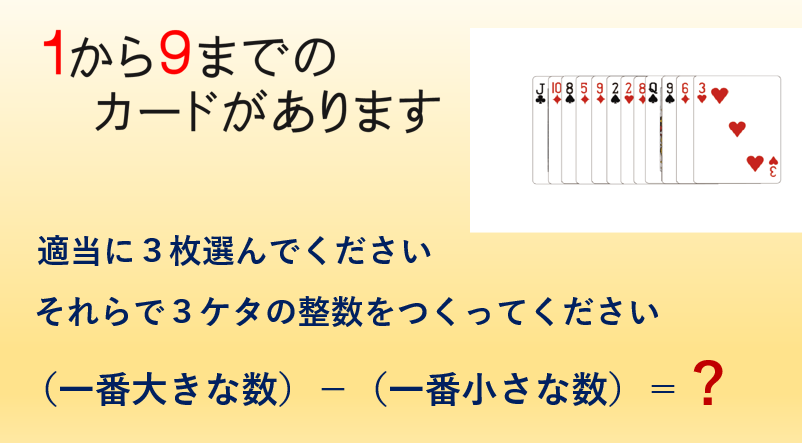

■ ところ:ある公立中2のクラス.教育実習に準じた形で特別授業が実施されました.大学3年生Rさんが登場.あいさつもそこここに,やおらトランプカードをポケットから出します.
■ 「ここに,1(エース)から9までのカードがあります.○さん,3枚ひいて,その数を皆さんに紹介してください.」
■ 「5,2,7」です.
■ 「ありがとう.○さん,その3数でできる一番大きい3ケタの整数と一番小さい整数を言ってください」
■ 「752と257です」
■ 「はい,そうですね.ではその2数を引き算してみて」
■ 「ちょっと待ってください」「495です」
■ 「ハイ,正解です.では次に●さん,同じように3数を引いて,さっきの計算をしてください.まず,その3数を紹介して」
■ 「9,3,6です」
■ 「ありがとう.その答えは,594になります」
・・・ハェー(速い)!,当たってる!の声・・・
■ 「皆さんもこのワザを身に付けたくないですか?ワケを理解して少し練習すると20分後には同じことができるようになりますよ.ヤルキ出てきたかな.では・・・」(略)
■ 「実は,{9,3,6} の場合,9-3=6 だよね.すると,100×6ー6 が答えになるんです.暗算でできますね.つまり,594です.」(以下,略)
計算式の背景

導入として◎部分

■ なぜ文字が重要なのか?これは,理屈や「説教」では効果はほとんど期待できません.むしろ文字嫌い・文字不信を生み,逆効果になることも.
■ 文字を使用しなければならない状況に学習者を立たせる必要があります.その状況は,シンプルで楽しそうなモノであれば◎です.
■ abc-cba ではなぜダメなのか?「100a+10b+c とやればうまくいく」では説得力に欠けますし,「この種の問はそうやるものだ」はヒンシュクものです.
■ 「100-1 を計算しなさい」はあったとしても,「99をわざわざ100-1 とする」思考の柔らかさが学習者に伝わってほしいですね.ただし,こちらから「解説してしまう」のは,推理小説で真犯人を教えてしまう行為と同じです.耐えましょう.
原題はコレでした

■ 原題は巻末や問題集で見掛ける,多少手こずる問題です.
■ 99(a-c) が出て終了,という無味乾燥な問ですが,この教材(食材)を,かなり魅力ある”料理”に変身させたという印象をもちます.
■ 教材研究とは何でしょうか.価値あるモノ(自然現象,観察や実験の結果,各種問題,課題研究からの問いかけ等々)を探り当て,かつ,そのモノを深堀りする必要があります.ネット等で出会ったモノを,何ら「調理」もせず安易にテーブルに出してはよろしくないですね.子供の目を軽視してはいけません.彼らは見抜いています.
■ 国語教育の実践家大村はまさんの教材に対する姿勢に,分野を超えた説得力を感じますね.
<追記>
■ 次回テーマは,「復習のありかた」です(予定).復習について今更アレコレ語ることはないだろう・・・ですか?復習=本来ならば「不要なこと」と考えると,どうしても「後ろ向き」になります.そこで,「前向きな復習」を考えましょう.
■ 本ブログの冒頭(エンドにも)に,「にほんブログ村」のバナーが2つずつありますが,それぞれClickしていただければ幸いです.


