紙折り10回挑戦

■ 紙(長方形)を次々に半分づつ折っていきます.
■ この紙折りですが,数学的には線対称変換であり,指数と直結します.また,高校で習う対数(log x) の「萌芽」もチョロリと見ることができます.
■ 指数は中1で学びます.その際,しょっぱな(導入)で「5×5を52 と書きます.同様に,3×3×3 は・・・」といった解説とお目にかかることもあります.率直に言って×です(いやx2 かも).
■ 新記号が登場する必然性や流れが見えません.したがって,子供たちに「新しいコトが提案されて,どんなことが出来るようになるのかな~」などいうワクワク感が生まれず,むしろ,負担感が増すような導入です.
何回折れますか?


Q1 A4の用紙を図のように半分に折ります.その半分にする作業を続けるとします.さて何回折れますか?予想してください.
また,折れ目で用紙を分ける(分割する)とき,折る回数とそのときの分割数(ピース数)の関係式を求めましょう.例:2回折り ⇔ 4分割
A1 切断と異なり,折る場合は,紙の厚さが折るごとに2倍になりますので,薄い紙であっても手応えというか,折らせまいとする紙の”抵抗感”が激増します.
物理的に折ることができる回数は,予想と異なる結果になるのではと思います.是非,トライを.
■ 折る回数と分割(ピース)数の関係ですが,帰納的に,1回:2,2回:4,3回:8・・・として導いてもよいのですが,発想からして「有限回までの話ですね!」と指摘されそうです(率直に言えば,稚拙です).
Ⅰ 折る⇒折れ線を付ける⇒合計ピース数は,それまでの2倍になる” ,Ⅱ1回目:2(ピース)
この表現は,高校数学で習う漸化式と本質は同一です.
このことから,折る回数とピース数の関係式は次のようになります.

何回折れますか
■ 実際に用紙を折ってみましょう.
■ いかがでしたか.
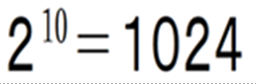
↑この式,気安く受け止めないで!
■ 紙を10回折って 1024枚にする ことは,そんなに簡単ではないことが分かりますね.
分かりやすい指数法則

17c 天文学者の寿命を延ばした計算法とは
■ 「天文学的数字」という形容があります.天文学では扱う数の桁数が大きく,計算が困難という意味です.17世紀のヨーロッパで,その計算負担を極端に減らし,結果「天文学者の寿命を延ばした」と評された計算法があります.それが「対数」です.
■ ここでは,そのideaの雰囲気を味わいましょう.
話を簡単にするため,計算途中で扱う数を{2,4,8,16,32,64,128}だけとします.
その際,下記のような一覧表(※)をあらかじめ作っておきます.

■ pointは,③で 32×128 は,実質5+7=12 の足し算で済み,④で 4096÷32は,実質12ー5=7 の引き算で済む ということ.
■ 5⇒32 と,7⇒128 とそれぞれ対応しており,底(テイ)を2として「5は32の対数」「7は128の対数」と言います.
→ それにしても,この対数(logarithm)という翻訳は名訳だと思いませんか.
※ この対数と比べると,有理数 という翻訳は誤訳に近いと思います(⇒ 有理数としたために,無理数の訳も誕生してしまった!).やはり,比が有る数,つまり,「有比数」とすべきでしたね.「比が有る数」ならば,分数形式という本質を突いており,かつ,無理数という暗いイメージの数も登場しなかったでしょう.これからでも遅くないので,是非,改名を進めてほしいものです.
提案: 有理数 ⇒ 有比数 無理数 ⇒ 無比数
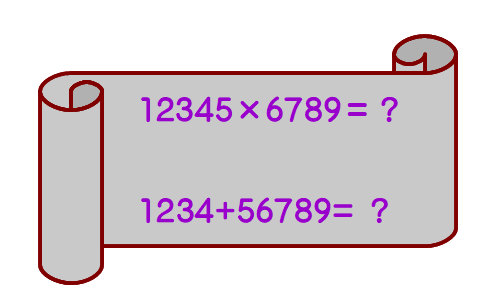
■ かけ算が足し算で,割り算が引き算で解が求められることは画期的でした.
手書きの場合,桁数の大きい数同士のかけ算と足し算の計算量を比較してみればよく分かりますね.「天文学者の寿命を延ばした」という表現はオーバーではなかったかも知れません.
■ ⑤⑥は,対数の基本定理です.
⑤は かけ算が足し算へ,⑥は 割り算が引き算へと導かれています.
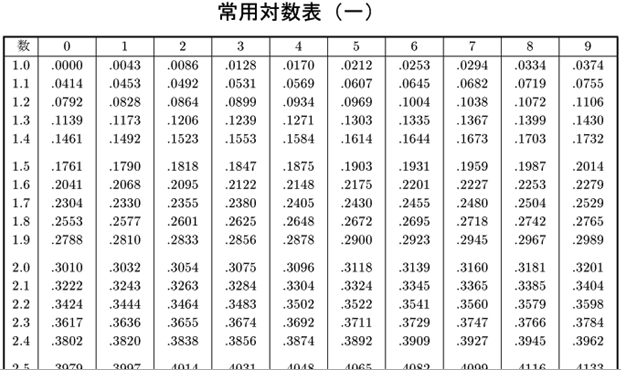
なお,任意の数同士の計算(※)のためには,対数の本格的”一覧表”が不可欠です.手回し計算機も,ましてやコンピューターもない17世紀,数学開拓者たちは心血を注いで一覧表を作成したことでしょう.参考までに一覧表(常用対数)の一部を紹介します.
※ 対数計算で得られる結果は,特別な場合を除き「近似値」です.
<補足>
■ 次回テーマは「量としての角」(予定)です.時計表示のデジタル化が進んだこともあってか,角の認識はサッパリです.
■ にほんブログ村のバナーをClickしていただければ幸いです.(最初:左,次:右)