「□÷0.8 」正解率,低っ!
■ 24÷6=4,18÷3=6 のように,割り算すれば,元の数(被除数)より商は小さくなる のだと思い込んでしまっているヒトは少なくありません.言葉自体が「割る」ですからね.
■ 「そりゃ,少数でしょう」と主張する方もいるかも.でも,後で紹介する全国学テ(小6)の結果をみると,そんなに甘くないことが分かります.
「算数」ではこんな問が
■ 小3算数
「15個のリンゴを3人に同じ数ずつ分けました.一人分はいくつになりますか」
⇒ 15÷3=5 一人分は5個です.確かに,15>5 ですね.この場合は,です.次はどうでしょう.
■ 小6算数
Q1 次の割り算で,商が小さい順に並べなさい.
① 24÷3 ② 24÷0.5 ③ 24÷2/3 ④ 24÷30 ⑤ 24÷0.2
答:省略(④最小,⑤最大)
Q2 全国学力学習状況調査(H28.4実施)

真の ”正答率” を推測する
■ Q2 の正解と正答率
正解:1 正答率:国の集計結果では65%です.
しかし,3択問題ですから,①分からなかったが偶然正解 ②分かっていたが不注意で誤答 の場合も考慮しなければなりません.
すると,真の正答率=65-①+② ただ,②はほとんど無視してよいでしょう.
よって,真の正答率 ⇒ 50数% ではないでしょうか.
■ 全国の小6生のうち,割り算の計算自体はともかく,半分近くは,割り算の意味理解が十分でないことになります.
■ 小3で割り算を習ったときの第一印象(割る⇒減)が強烈なのでしょう.擦り込みともいうべき状態ですね.
しかも,この擦り込みが,後に,彼・彼女の数学人生を暗くさせてしまう一因となるかも.
「1÷(0に近い数)」のイメージがわかないと・・・
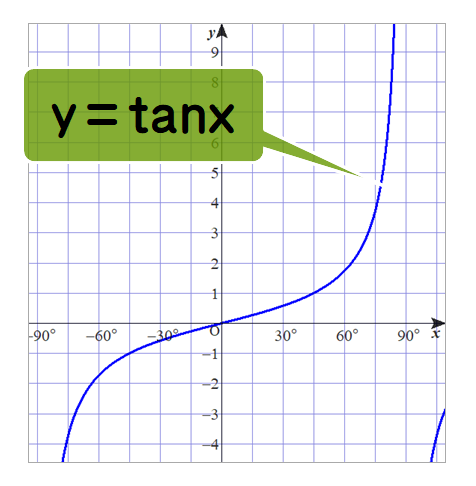
■ 順不同になりますが,
①まず,tan90° (形の上で 1/0 )の理解でつまずき,結局,「値なし」を棒暗記することになります.
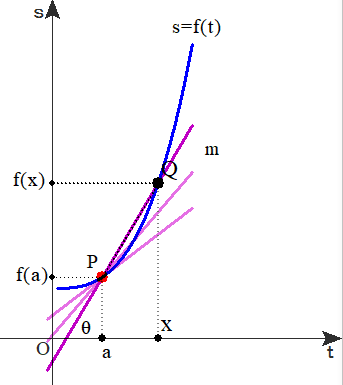
②微分係数=「任意の点における接線の傾き:f'(a)」という定義から微分はスタートします.
f'(a)を求めるとき,極限計算をするのですが,その際,0/0という不定形の極限と遭遇し,tan90°のときと同様の場面が登場します.
■ ①②をクリアするための共通必須アイテムは「1÷(0に近い数) のイメージ」です.このイメージを持てずに微積分を理解していくのは,経験則から言えば,極めて困難で,いきおい暗記数学に向かいます.
1÷(小さい数) ⇒ 1問ごとの正誤より”流れ”の体感を
■ 児童生徒には,「1/0.02=50 ,合った!」などと,単問として見てしまい,その○×だけにとらわれないでほしいと願います.○×結果が学習の動機付けになること,否定しませんが,邪道ですね.いずれ限界が生じます.主眼は,割り算しても,答(商)がもとの1より大きくなる,そういった体感&実在感を得ることです.
■ 反比例のグラフを,以下のように発展・有効活用をしましょう.教科書範囲外と排除することなく,「教科書を」でなく「教科書で」の精神で.
■ 「実数の稠密性」をもにらんでイメージ化させたいもの.計算のすべてを手計算するのは時間掛かりすぎですから,適宜,電卓の使用が現実的ですね.
y=1/x のグラフはどうやって描くのか
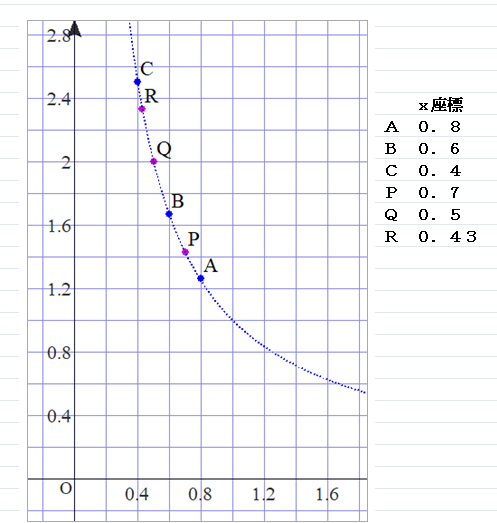
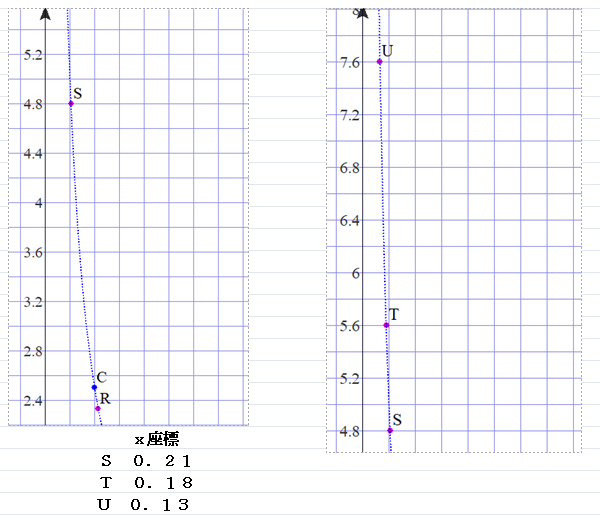
■ 反比例:y=1/x のグラフの扱いについてです(小6,中1).まず,肝心な部分のボカシが目立ちます.
①数点をプロットするのみで,それらを突然,実数線で結び滑らかな曲線を描くのは,仕方ないところもあるとは言え,飛躍・反則です.思考の入っていない,当初から曲線ありきの作業になっています.
②x軸,y軸が漸近線になるわけですが,特に,y軸についての言及がおざなりというか,中には全く説明せずに進める光景も見受けられます.このツケが数年後に何倍返しで襲ってくるのです.
■ 左(上)図では,9点プロットしましたが,1/0.1 の表記は難しいし,ましてや 1/0.01=100 という例もスペースの関係で示せません(小中では,軸の尺度は1:1としているようです.理科や社会では自由ですが).y軸の途中にカット線でも入れて,xが小さくなるにつれて,yの値がぐんぐんと上昇する様子を描いてほしいものです.
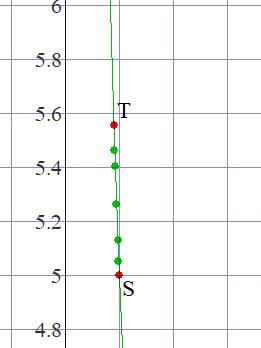
■ たとえば,点ST間にはxとして,0.183, 0.185, 0.19, 0.195, 0.198 等々,いくらでも数を”指名”でき(⇒実数の稠密性),それに応じてyの値は計算できます.
■ この”点だらけ”状態 ⇒ 曲線状に並ぶ ⇒ 点を無数にする ⇒ 曲線(双曲線)が形成される,こういった様子をイメージ化し,その上で,1/0.02 などの値を再認識させたいものです.
鬼門「1÷0」 はどう乗り越えさせますか?
■ 「x→0(正) のとき,1/x → ?」は 本質において,tan90°=? と同値です.したがって,小6で三角比・三角関数の序論に入っているワケです.換言すれば,小6でも tan90° の言わんとするところに触れていますので,そのチャンスを逃すべきではありません.
■ 大別して2とおりあるようです.
① 1÷0 のように「0で割ることは出来ない」の説明 ②反比例(双曲線)のグラフによる説明
①は,1/0=a とおき,分母を払う形で 1=0 の矛盾結果から説明しますが,暗に背理法の利用があり,また,グラフが登場しないので,どことなく釈然としない雰囲気が残ります.
② 1/0.1=10, 1/0.001=1000, 1/0.000001=1000000,・・・ と yの値はいくらでも大きくなる, グラフの状態でイメージすれば,際限なく上方に伸びるので,結局,「値は定まらない」となります.

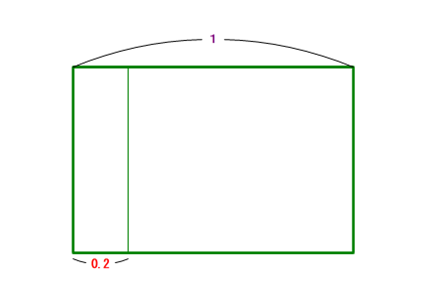
■ 仮に,1/0=∞(無限大) ③ とすると,次のような「困ったこと」が生じます.
・③で,分母を払うと,1=0×∞=0 となり,矛盾!
・また,∞+100 という式を考えます.無限大に100を加えたって,無限大です.つまり,∞+100=∞ ゆえに,100=0 これまた矛盾!
・以上のことから,∞は数ではなく,「状態」を表す記号と捉えておきましょう.まぁ形容詞ですね.
・左(上)図が,1/0.2 の意味でしたね.すると,1/0.01 ,1/0.001も図で見当がつくようになるかも.計算の前の,図理解です.
<補足>
■ 次回テーマは「学習の進んだ子供part2」です(予定).「素数が無限にある」ことの証明は,背理法を用いることもあってか,今一つしっくりこない向きもあります.ある中2生がそのモヤモヤ感をスパッ!脱帽です.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


