やはり 0.999・・・=1 は疑問?
■ 0.999・・・=1 については,いつの時代も世代を超えて話題になります.
ということは, 今日でも,ナットクのいく解釈・解説が不十分 という証左かも.
■ 数学セミナー(‘19.11)で,数学界大御所の一松信氏(京大名誉教授)が取りあげていましたので,認識を新たにした次第です.

やや 無理筋 の説明
A1

■ 手短で説得力に富み,ナットクするヒトも少なからずいます.しかし,多くの数学関係者が指摘するようにムリがあります.有限小数の0.333333×3は計算が可能.しかし,末尾が永遠に続く①「・・・」の部分を3倍するという計算自体が?です(繰り上がりがないからokとはいかない).
■ こう言っては語弊がありますが,1=0.999・・・には「ナヌッ?」と感じたとしても,1/3=0.333・・・なら抵抗感が少ないだろう,みたいな安直さもチョロリと見える説明ですね.
A2

■ これも「・・・」部分の引き算をしていますので,A1と同様の評価が避けられません.引き算なのでかけ算よりはマシだろうという声も出るかな.
そもそも「・・・」の意味は何?
■ 小5算数教科書より
「 △/□=△÷□ より 2/3=0.666・・・ 」という解説が突然出てきます.
このように,分数 を小数展開する際,割り切れないとき「いくらでも続く」を表す意味で「・・・」という記号を使っています.日常用語の延長で「ワカルでしょ」くらいの扱いでしょうか.
■ 高校数学Ⅲ教科書より

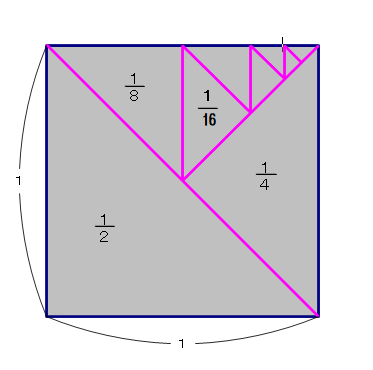
図は,① 1/2+1/4+1/8+・・・=1 についての,正方形の分割による図形的な説明です.
①の左辺を小数で示すと
0.5+0.25+0.125+・・・ ですが,
この場合は「チリも積もれば山となる」は成立せず,総面積の1を超えられないことが図からも説明付きますね.
■ 以上をまとめると,「・・・」は
日常用語として,”延々と続く”という意味で使用(例 1/3=0.333・・・).情緒的な側面が濃い.
高校数学では,無限級数における極限計算の中で使用.情緒面をベースにして”数理”上の意味と扱いを明確にした.
改めて 0.999・・・=1 をどう考えましょう
■ 本問の核心は次の3点の確認かと.
①ひたすら長く続く0.999・・・が一つの実数aを表していることを理解・体感する
②極限値計算(収束公式)により, a=1 となる
③再度,①に戻り,0.999・・・=1 であることを再認識する(”しみじみと感ずる“)
なお,a=1 の証明については上記の外,「0.999・・・と1の間に実数があるとすれば」という仮定のもと,背理法により a=1 と示す方法などが知られています.いずれにしても上記①③の確認が必須の用件ですね.
A3

0.999・・・ が一つの数を表す:ダメ押し
■ 0.999・・・が一つの数を表す根拠理由を探してみました.
それは「有界な単調(増加)数列は収束する」※という公理(基本の基となる約束事)です.この※がないと実数軸は穴ボコだらけになってしまいます.
例:1, 1.4, 1.41, 1.414,・・・ この数列は,√2 に収束することになるのですが,認めないと実数軸上で√2を示す点に「アナ」が空くことになります(不連続点).
このように※は,実数の連続性を保証する公理です(なお,同値な公理は複数あります).
■ ところで,数列{Sn}は,上に有界な単調増加数列です(0.999・・・という式の作りからして1を超えることはなく,増加は明らか).
すると,公理※により{Sn}はある値aに収束し,極限計算によりa=1 となります.
<補足>
■ いろいろ述べてきましたが,でも,0.999・・・<1と主張するヒト,やっぱりいますよね.
■ 次回テーマは,「宇宙人はいるか?」(予定)です.最近,結構話題になっていますね.やや視点を変えて取りあげたいと思います.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).