面積を測る:タイヘン!
量の中で,距離,重さ,温度,角度などは,それぞれモノサシ,秤,温度計,分度器という身近に見られる道具で計量することができます.しかし,面積については,どうでしょう.
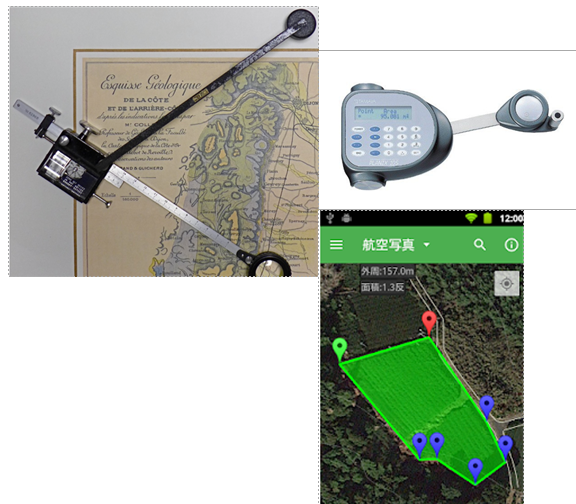
プラニメーターという面積計があります.図形の輪郭(りんかく)をなぞって1周すると面積を計測できるというプロが使用するもので,価格も結構します.アナログ式精密装置であり,教室内で子どもたちが遠慮なく使えるような教具ではありません.
スマホでは,地図上の閉じた形の面積を表示するアプリや画像dataから距離や面積などを計量するアプリが開発されており,その機能に驚かされます.ただ,これらアプリは屋外での測量をメインにしたもので,ノートに書いた図形の計量などは対象外と思われます.
ヒトの量感覚・・・長さ○ 広さ? かさ×
長さ(距離)は,1次元量ですから,主に直線上の長さ判断による量の把握が容易です.モノサシが最も基本的ツールです.
では,広さ(面積:2次元量)はどうでしょう.
Q 下図のように,2つの三角形があります.どちらの面積が大きいでしょうか?

A目盛りを数えると分かりますが,底辺の長さと高さが同じですので,面積は同じです.
何人にたずねますと,答えはまちまちで,左の鈍角三角形の面積が大きいと答えるヒトがやや多いようです.
このように,広さという2次元量の直感的理解・把握はかなり怪しくなります.体積など3次元量となると困難度は一層増します.ドラム缶1本の水量はバスタブ(家庭用)の何杯分くらいでしょうか?(答は後ほど).
量感覚アップの工夫
量感アップするための工夫がされてきました.
基本になったのは,量感把握がほぼ安定している別の量で置き換える方法です.
例1 温度の測定
昨今はデジタル式が大半ですが,かつてはアナログ式の寒暖計や体温計がありました.それぞれガラス管内に密閉されたアルコール,水銀の膨張の度合いを目盛りで確認して温度を測っていました.
すなわち,目盛り読み取り ⇔ 1次元量把握
例2 重さの測定
秤(はかり)が発明されました.天秤やバネ秤がその代表です.原理は,重さを釣り合わせて,その時の目盛りを読み取ります.
つまり,目盛り読み取り ⇔ 1次元量把握

このように,一般のヒトビトの量感を向上させるため,さまざまな量を 1次元量”長さ”に帰着させる方法で対応してきたと言えましょう.
量感の基本・・・大小関係
量感醸成の第一歩は,何と言っても大小の区別です.これは原始の時代から,食料の確保・分配のためリーダーの必須判断能力であったことは,想像できますね.
今回のテーマ:面積測定に戻ります.
教室内で気軽に使用できる面積測定器がないとすれば,せめて,面積の大小だけでも「体感」させたいもの.
重さの測定はタイヘン!
面積を測る際,厚さは無視します.
そこで,均質な材料で”見える化された面積”であれば,その大きさは重さに比例
つまり,面積 ⇒ 重さ測定 と変換可能
具体には,図上の2つの三角形を下図のような計量計でそれぞれ測れば,重さ比較から面積の大小が判断できますね(この場合は,同じ重さ⇒面積も同じ となるハズ).
ただ,実際にボール紙で三角形を作り,カッターナイフで切り抜く作業をすると分かるのですが,同じ重さを示すような,理想的な切り方というのは極めて難しいのです!.また,均質なボール紙使用も必須条件です.

下の製品は,0.01g単位刻みで測定可能

手作り測定器で十分!?
面積測定のため,重さに帰着させるideaはすばらしいですね.しかし,重さを測定する実際となると,切り方や材質の均質化など,そのための条件整備が大変で,本末転倒の事態も発生します.
そこで,機能を大小比較だけに絞った,素朴な教具を作ってみました.

ベースとしたのは,天秤です.しかし,化学で使用するような精密天秤にはご遠慮願いましょう.
㎎単位の重さを測る機能を持っていると,それに見合う図形を用意できないからです.
用意する材料は,①割りばし ②クリップ ③つまようじ ④糸 です.瞬間接着剤もあった方がよいでしょう.
下図のように,最初に,バランスを取った状態はしっかりと示すことが必須です.
なぜなら適当な割りばしを使用しているため,中点が重心とは限らないからです.水平バランスが取れたことを確認した上で,左右に重さを掛け,それらの重さの大小を目でナットクしてもらうワケです.

各部分を拡大してみます.糸とクリップの接点などには,適当に接着剤を付けます.
図形をクリップに挟んでぶら下げると左右のバランスが一定しません.クリップに横幅があり,支「点」にならない ⇒ 図形の端に小さいホールを空けます.クリップ先端部を少し外側に曲げ,そこをホールに通してぶら下げると,ほどほどの支点となって,バランスも取りやすくなります.

三角形面積公式のナットク

完全な水平にはなっていませんが,おおよそ左右の重さ,すなわち,面積が一致していると読み取れますね.

積分による面積公式のナットク
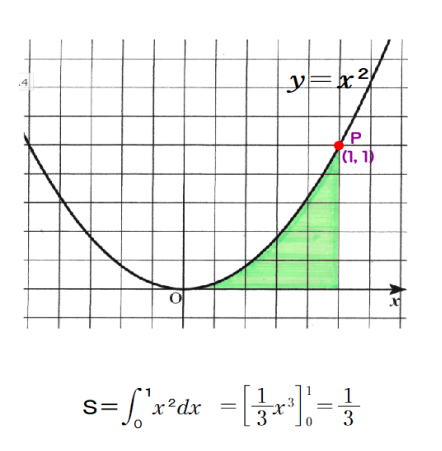

※ 右図は,画像ソフトgrapes(フリー)を使用.100円ショップで購入した工作用紙に直接印刷してカッターナイフで切り抜いたモノ.曲線部はハサミの方がよいかも.
上記の右図形は,曲線と直線で囲まれた部分で,その面積値は近似値ではなく,ジャスト1/3であり,左長方形の面積と一致します ⇒ ほとんどのヒトは右図形が大きいと言いますね
この事実に,不思議感を抱きましょう.積分計算で面積が求められるとは!
18cの発明・発見(微積分)を簡単にスルーしてはもったいないですね.

<補足>
■ バスタブの件:ドラム缶は1キロリットル,バスタブの大きさもいろいろですが,200㍑~300㍑くらい.したがって,ドラム缶1つで4バスタブ分くらいの量になります.
■ 「ある図形の面積がその重さに比例する」ことが理解されるかどうか.この気付きこそが,むしろ重要とも言えます.重さの測定で面積の大小が判定できないケースとはどういう場合か,是非,考えさせましょう.
■ 次回テーマは,「y軸の意味」(予定)です.算数・数学の教室で,y軸軽視の傾向が強すぎます.言っている意味が不明? 失礼ながら,それは,これまでy軸の扱いがぞんざいだったからでは?
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).