座標は”道案内”(小4)から
小4で「位置の表し方」を習います.つまり,簡単に言えば”道案内”です.日常でよく目にする道案内ですが,数学の土台を形成する座標概念の第一歩になります.
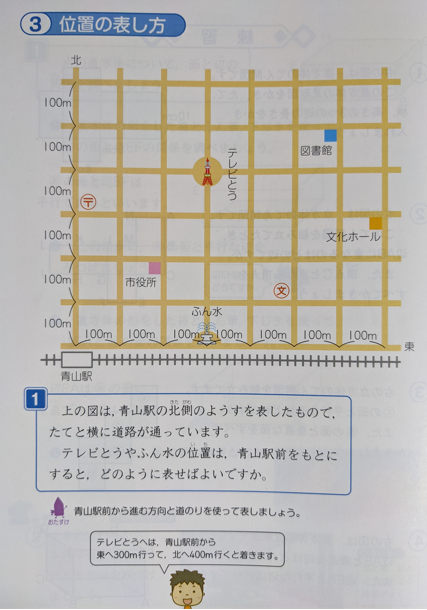
小4算数(啓林館)
■ 代表的な道案内3例を紹介します.
道案内(Ⅰ&Ⅱ)
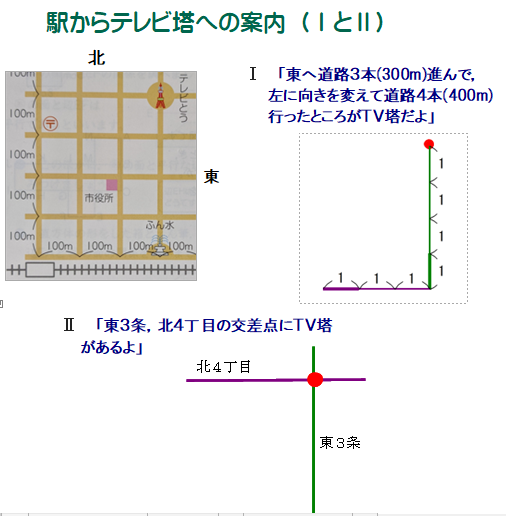
■ さほど違いのないように見えるⅠとⅡですが,算数・数学のリーダーは,この「違い」に鈍感であってはなりません.
<ⅠとⅡの違い>
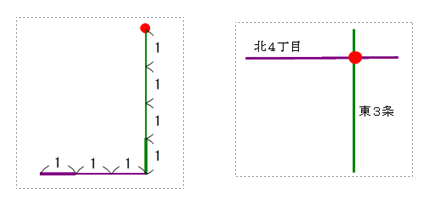
■ Ⅰ(左)とⅡ(右)を比較して,より基本(原型)に近いのはどちらでしょう.
Ⅱは(東3,北4)と書けます.端的でスマートですね.しかし,市全体の道路が碁盤の目のように配置されていることを,あらかじめ知っておく必要があります.
Ⅰは,どうか.その町にさほど詳しくなくとも,指示通り歩けばよいのです.
したがって,原型は,“断じて”Ⅰになります.中高数学の座標に絡んでつまずいた時は,原型Ⅰに戻ることが大切です(この部分,後述).
■ Ⅱは,xy直交座標の導入部分となります(中1数).
■ ところでⅠ,Ⅱよりさらに「原始」的な道案内の仕方(Ⅲ)があります.幼児でも十分使いこなしていますよ.
道案内(Ⅲ)
「市役所はこの近くかな?」
「あっちの方.すぐ近くだよ」
■ 幼い子どもの道案内では最もありそうな例です.あっち・・・指先(「北へ」のように方位を用いることも)が向きを示す.すぐ・・・距離(or時間)を示しています.
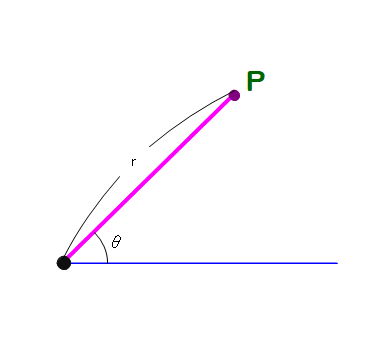
■ 今いる地点から,基準線からの向き(角θ)とそこまでの距離(r)で目的先Pが決定しますね.
■ 位置Pを(r,θ) とかき,点Pの極座標といいます(高校数学後半).
■ xy座標との関係は,図から分かるように,x=rcosθ,y=rsinθ となります.
■ 一番素朴と思える道案内の術(すべ)が,数学では,極座標として高校数学の最終面で登場するのは何とも面白いですね.
道案内Ⅱの補足
■ 道案内Ⅱで,TV塔(東3,北4)を例に挙げました.子どもの理解度を推測しますと,
(東3,北4) ⇒ TV塔 〇 ですが,
TV塔 ⇒ (東3,北4) ?× です.
つまり,座標を見て,点をマークする,はよいのですが,点を座標で表すことに抵抗感をもつケースがあります.
単なる逆対応でしょ,そんなコトないでしょう!?.ところが,実際に座標を扱う段になるとケッコウつまずきます.次の例をみてください.
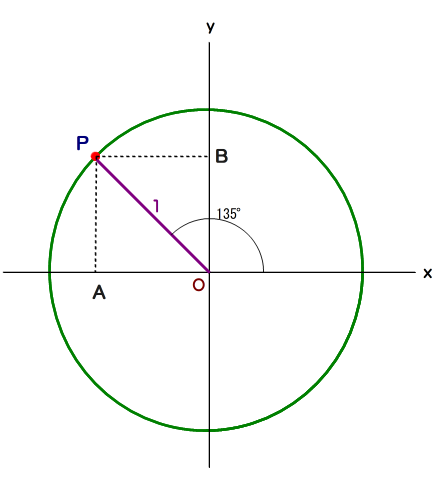
■ 半径1の円(単位円)の周上を動点Pが反時計回りに動いています.点Pが図の位置になったとき,Pのx,y座標を求めましょう.正に,「点⇒座標」の問です.
■ つまずき例とそのワケ
①意味が理解できない・・・突然の円に驚いてしまい,座標が目に入らない.ましてや「道案内」のことなど思い出せない.
②P(-0.5,0.5)・・・∠AOP=∠BOP=45° つまり,直角の1/2 のため,PAも1の半分,よって,PA=0.5
③P(√2,√2)・・・三角定規(1:1:√2) の比をソノママ使い,また,長さと座標の区別がついていないため x>0 としている.
■ <対応策&グチ>
①道案内の原点に戻る.OからAまで進む,右折してPまで上がる ⇒ 西1/√2条,北1/√2丁目
②③図からして「PA=0.6~0.8」と判断する眼をもつべし,ですね.どう見ても PA=0.5 はおかしい!と感じなければなりません. 長さの大小比較は算数以前の必須能力.
※ 1/√2≓0.71 いう量としての認識もなく,sin135°=1/√2 ,cos120°=-1/2 などと,ひたすら三角比の値を棒暗記するヒト,要注意です.一事が万事,その姿勢が数学を自分から遠ざけています.棒暗記してきた少なからずの学生を見るにつけ,さてどこから手を付けようか?と悩みは深かったです.
<補足>
■ 次回テーマは,「13日の金曜日は年に何回あるのか?(レポート)」(予定)です.”学習の進んだ子ども(第3弾)”です.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


