“記号”を味方に!
「数学は記号の学問である」と言われています.確かに,数も記号,演算(+, × , y’ ・・・)も記号.だから,数学は世界共通”言語”なのでしょう.この記号を”敵”にしてはなりません.
「記号は”約束”にすぎない」 との声?
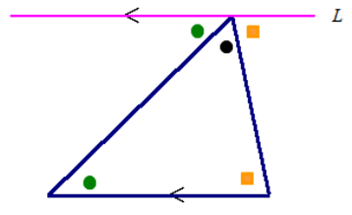

■ 図形の問題等で,補助線1本付け加えるだけで証明が即,解決する場合がありますね.
図は,三角形の内角の和が180°の証明です.補助線Lを引くだけで一気に解決します.
それに比して,記号の意味や意義などは,しょせん,約束ゴトであり,本質ではないのでは?とのご意見もありそう.
しかし,123×456 を和算式で計算してみてください.いかがですか.
■ 今日,小6生のほとんどは,123×456 を計算することができるでしょう.しかし,200年ほど前まであれば,日本人のほとんどにとってムリ,というか,そもそも計算を必要としない日常であったのです.
■ 当時,算術の達人がいても,上記の計算は「超難問」だったでしょう.なにしろ,0の概念がなく,また10進法に基づかない漢数字の使用ですから.
■ この例は,すぐれた記号 ⇒ ヒトビトの思考を深めるツールになりうる を示しています.
すぐれた記号たち・・・改めて”感心”します
■ 記号の意義

次の2点を挙げます.
①思考の対象が,簡潔な記号を使用することで一義的に限定され,他とも共有することで思考がより深まる ⇒ 「記号の記号化」が進展する
②記号を用いた公式は,簡潔で明白な世界共通の文章である(少しオーバー?).
■ いくつかの記号で確認しましょう.
(1) ×記号
■ 4の5つ分:4+4+4+4+4 は長いので,これを 4×5 とする,ということ.
アルファベットx と間違いやすく,ヨーロッパでは「・」が普及しているようです.
■ この記号により,九九が登場します.
ただ,意味も分からず九九表を「棒暗記」する・させているシーンもありますね.
「かけ算の本家はたし算」という根本をタイミングよろしく確認していきましょう.
高校数学「場合の数」で,和の法則と積の法則を扱いますが,これらをベツモノとして受け取っているヒトが少なからずいます.残念!
<乗除は加減に先立つワケ>
Q1 8+2+2+2+2+2 を計算しましょう.
Q2 2+2+2+2+2 は長いですね.普通,どのように書きますか?
8+2+2+2+2+2 を短く書いてください.
Q3 8+2×5 = 10×5=50 のおかしいところはありませんか?
(2) 分数記号
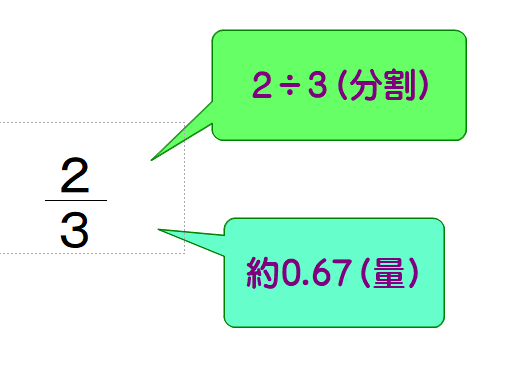
■ 2/3 はよくよく考えられた表記だと感じます.何しろ,二つの意味を同時に示していますから.
①分割分数・・・2÷3という操作
②量分数・・・約0.67 という数量
■ 「なるほど感」のpointは,”2と3で,新たな数:2/3 を創っている“という視点を理解することです(子どもに伝える必要はありませんが)⇒ 後に.√3 や0.999・・・etcの導入の際も,”数を創る”という同じ姿勢で対応できます.
<ご案内> 当blogに訪問ください↓
https://math-negi.jp/fraction-type/
(3) Σ記号
■ Σ(シグマ)は,加算の記号です.1+3+5+7 程度だと意味ないのですが,数の個数が20,50,100,さらには,無限個になる場合にはその“御利益”が実感できます.

※ 和(sum)の頭文字:sに対応するギリシャ文字がΣということがこの記号の由来とか.
もし,日本が数学発展の中心だったならば,今頃は,Σではなく,「和」という文字を当てていたかも(ないか!).
■ Σ記号については,”分配法則”や”定数倍法則”などの性質がラクに証明され,それらが威力を発揮します.実際,Σ記号抜きにして,微積分の理論構築は困難でしょう.

■ 一般項をゲット ⇒ その一般項にΣ記号をかぶせると,第n項までの和が機械的に求まります.階差をとってみるなどという手間が不要となります.
疑問のある記号
■記号=すべてよろしい というワケでもありません.基本の基である「-」記号など,その代表です.
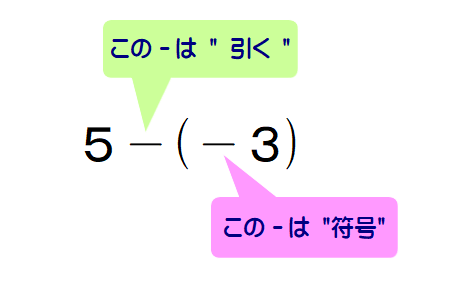
■ 「-」について
①演算(operation):”引く”,②符号(sign):負 の二つの意味があって,しかも,同時使用されていますので,これは習う方も教える方もタイヘンです.
■ 昭和時代の教科書(中1)はかなり大ざっぱでラフな記述がなされています.今の教科書はかなり気を配っての解説となっています.
5-(-3) は,「借金3円が引かれる=3円得する」の意味.よって,5-(-3)=5+(+3) となる.ここで,カッコ前の+は,省いてもよいとすると,5-(-3)=5+3 と書ける(ここまでのところ,+はsignマークです).
こんな感じの解説ですが,かなり苦しい説明となります.結局,-や+記号は,演算と見ても符号と見ても,ルールに従っていれば”結果オーライ”という感じでしょうか(妥協!).
←小学校で習った 5+3 の+は,演算ではなく符号(sign)だった?そんなハズはないですよね.どう整合性をとるのか・・・
便利すぎる記号には要注意
■ 記号の扱いでもっとも気になるのは,類似している記号のよさを逆手にとって,論理を軽視(or無視)して論を進めているケースです.それも,小中高を通して算数・数学の集大成とも言うべき「微積分」で散見されますので,ナントモ情けない限りです.

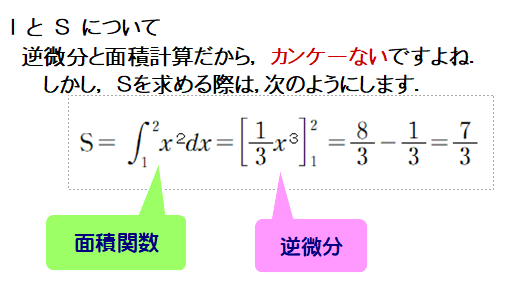
■ 「面積を求めるには,逆微分=積分を用いる」⇒ この結論の大元こそが
微積分の基本定理
です.どの教科書にも載っていますが,やはり解説は難しいです.興味を示す生徒もごく少数でしょう.
だからといって,まったく概念の異なる2つの∫記号が似ている(⇒先人たちの配慮!)ことを以て,解説のスルーはよろしくありません.一事が万事,”困難スルー指導“に陥ります.
<補足>
■ 記号の使用の際は,創った・作った先人に「思い」をいたしましょう.
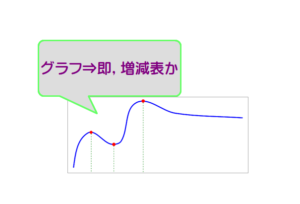
■ 次回テーマは,「増減表の解釈」(予定)です.微分で増減表を作り関数のグラフを描きます.この増減表ですが,ケッコウ奥が深いのです.
■ にほんブログ村のバナーをそれぞれClickをしていただければ幸いです(最初:左, 次:右).


≪…「-」について ①演算(operation):”引く”,②符号(sign):負 の二つの意味…≫を、
自然比矩形( 1×(e-1) )の(-1)を演算か符号かを・・・
ヒフミヨはながしかくにて式創る
この物語は、絵本「もろはのつるぎ」の図形のヒミツ・・・
-1は数学時間ヒフミヨに
なんか?! ➂ の意味を浮上させたいです・・・
ヒフミヨ様
地味な拙blog にコメントいただきましてありがとうございます.
ただ,当方の理解力不足もあり,率直に申しましてご返答に困っています.
「-」について,ア 演算(operation),イ 符号(sign) 以外の意味を構築したいと言う趣旨でしょうか?
よろしくお願いします.
あ北のネギボーズ
≪…「-」について,ア 演算(operation),イ 符号(sign) 以外の意味を構築したいと言う趣旨でしょうか?…≫を、自然数 [0] 整数 の離散的通過点表示を実数直線で眺める『幻のマスキングテープ』で[奇数]+[奇数]は[でんぐり返り](反転)の[-1]を掛けるコトに[無意識]に内在化してしまう。
数の言葉ヒフミヨ(1234)は、[-]の世界からの送りモノかもしれない?・・・
令和6年4月に開設の岡潔数学体験館で、自然数のキューレーション的な催しがあるといいなぁ~
コメントありがとうございます.
「ア演算,イ符号 以外の意味を構築したいのか?」についてです.
学習者(中1)の立場で教科書を読み直したとき抱いた感想・疑問でした.習う方も,教える方もタイヘン!
したがって,ご指摘のような深い・高い水準からの話題提供ではありませんでした.
昭和の古い事典ですが,数学小辞典(矢野健太郎.共立出版)では,「符号」の項目の最後に「数式の中では,加法記号+,減法記号-と正の符号+,負の符号-がしばしば混同して使われる」と解説しており,妙にナットク(諦め?)しております.