サイコロはフェアか?
20年近く前,身近な教具であるサイコロをしげしげと見つめ,再認識いたしました.ある新聞記事をみたことがきっかけです.


■ 本blogでは二度目の登場になりますが,入曽(いりそ)精密製(入間市)の超精密サイコロを話題にします.

(2004?.12.9 産経)
5の目が出やすい?

■ 記事の中で,入曽精密の斎藤社長は「(普通の)サイコロでは,5の目が出る確率が高い」と話しています.
■ 目は彫って形成します.その際
1の目はサイズがやや大きい → 次に彫りが少ないのは2の目 → 2の目近くの材料容積が多く残り, 転がすと重さで下になりやすい → 対面の5の目が上になりやすい
と解釈しました.
■ 実際は,粗雑なサイコロもあり,いろいろなケースがありそうです.最近知り得た自由研究報告(中2生)によると,5000回振ったところ,4と5の目が多く出る結果(順に17.6%,17.3%)となっています.最小は2の目の15.7%という内容.
→ 総合的に考えると,重心が2の面にやや近いのではないか,という推測ができそうですね.
正しいサイコロは存在しない
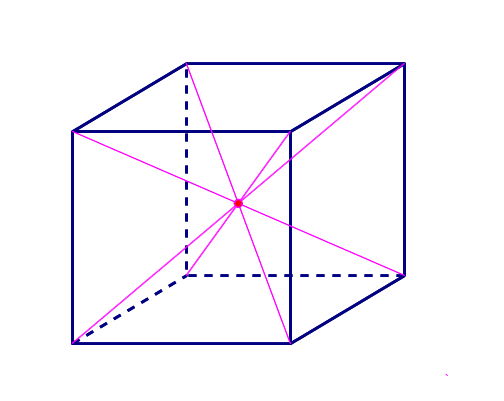
■ 正しい(理想の)サイコロとは,
Ⅰ 素材が全く均質の材料からなり
かつ
Ⅱ サイコロの中心と重心が一致する
の2条件を満たす必要があります.
■ 冷静に考えると,材料が均質で,重心に偏りがない「理想サイコロ」は,サイコロが物質である限り存在しません.物理的に不可能なのですね.世界各地にあるm原器が,”1mジャスト”ではないことと同じです.
■ したがって,サイコロの製作に当たっては,理想サイコロにどれくらい近づけられるか,が指針になります.
材質の均質化はハードルが高いので,ここでは重心の調整を考えてみましょう.
「同様に確からしい」は当然か?
■ サイコロの目はどうやって作りますか?大別して,①彫る,②ペイントを塗る,③その両方 があります.
どの方法でも微量の重量変化が伴います.微量であっても,重心の偏りを極力小さくしなければなりません.次は1と3の目の場合の一例です.
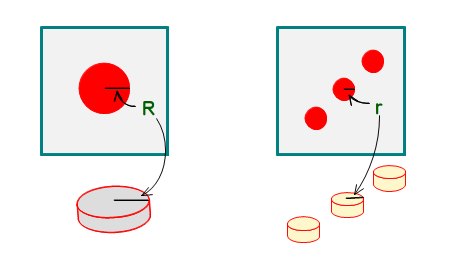

■ カジノゲームのクラップスや競技バックギャモンで使われるダイス(サイコロ)は、少しでも重心の偏りをなくすため、目を凹ませた後に素材と同比重の塗料(もしくは本体と同材質異色の材料)で埋めてあるそうです.これらをプレシジョン・ダイス(precision dice、精密ダイス)といいます。(この項 Wikipedia を参考)
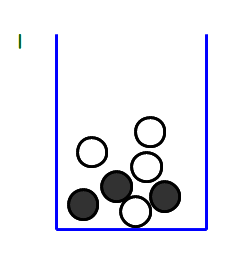
■ 袋に石が入っており,そこから任意に石をとるという試行があります.石の形・大きさ・重さが同じで,表面も滑らかであれば,サイコロの目の出方と比べると,ある色の石が取りあげられる確率ははるかに「同様に確からしい」ですね.
識別が石自体ではなく,色という属性にあるからでしょう.
■ 「袋に白球4個,黒球3個が入っており,同時に2個を取りあげたとき,2個とも黒である確率を求めよ」という問題があります.もちろん解は,₃C₂/₇C₂ (≓0.143)となります.
■ 大数の法則を皆で実感しようと,白黒の碁石7個を入れた封筒を8袋を用意しました.クラスを8グループに分け,各グループごと50回ずつ試行して,クラス全体として計400回の結果を求めて,理論値0.143との近さを「味わう」という目論見です.
■ しかし,よい結果が得られません.なぜでしょう.
→ 布製の袋でなく,長方形の紙封筒に原因が・・・.
2隅に碁石が「固定」されるようなグループがいくつかありました.そこで,隅を折って改善を図りました.
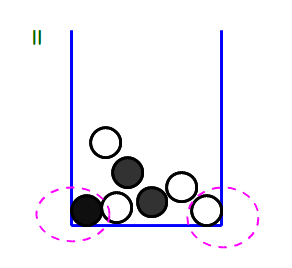
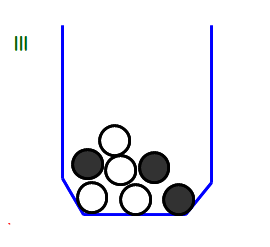
■ このように「同様に確からしい」とサラリと簡単に言ってしまいますが,実際は,その状態をセッティングすること自体が苦労を伴うものなのですね.
■ 「物体と斜面の間には摩擦がないものとする」という言い方を理科や物理の教科書で拝見します.
「スミマセン.ホントはこんなことはないのですが」という思いというか,謙虚さが感じられます → 摩擦を考慮するとどうなるの?という発展に繋がります
その意味で,数学の記述には「同様に確からしい」に限らず,反省するべき点が多々あると思います.
入曽精密製サイコロ
■ 入曽精密のサイトから一部紹介します.

世界最速のサイコロ(完全版) ~世界一フェアなサイコロ~
「世界最速のサイコロ」の最終進化形です
ご要望により再生産決定!
3 次元上のサイコロの中心点と各面の距離の誤差は2.23 ミクロン以下に収まっており、世界最高と言っても過言ではない精度を誇る「世界最速のサイコロ(シェイプ)」。
しかし我々はこの現状に満足せず、さらなる高みを目指した結果、” 完全版” 謳うに相応しい精度の達成に成功し、ギネスブックに申請中です。「世界最速のサイコロ」の最終進化形です! ・
【特徴】
■重心が限りなく真ん中に近いサイコロ
立方体を6つの四角錘に分割して考えた場合、底面に彫られた6つの目の形状を調整して、それぞれの四角錘の重量が均等になるように削ってあります。6つの四角錘を組み合わせたとき、設計理論上中心から各底面までの距離の一致度は99.99999999%。
■目の彫り込みについて
目の彫りこみをできる限り浅くして、空気抵抗を極限まで抑え込むことに成功。
■サイコロ全体の質量特性
・ 材質 チタン
・ サイコロ角 12ミリメータ
・ 密度 0.00451000グラム/立方ミリメータ
・ 質量 7.65818グラム
・ 表面積 1902.660平方ミリメータ
・ 体積 1698.045315立方ミリメータ
■高校の教科書でも紹介
このサイコロは、高校の数学教科書の確率論の箇所に画像が引用されました。
※詳しくは 株式会社入曽精密へ
<補足>
■ 次回は,「大学共通テストへの注文」(予定).注文と言っても内容ではなく,マークシート選択肢の在り方についてです.
■ にほんブログ村のバナーをそれぞれClickしていただければ幸いです(最初:左, 次:右).