整数方程式の”源流”

整数方程式 5x-13y=1 などは，ごくありふれた問題で，解くことも「楽勝」でしょうが，少し立ち止まってみましょう．

Q1 整数方程式 5x-13y=1 を解いてください．

x,yなど未知数が2個の場合，通常，方程式は2本必須です．しかし「x,yは整数である」という条件が付くと，式の本数が1本でも解が求まることがあります(解がないときも．後述)．

A1 次は，定石による解法です．

整数方程式が解けた！でジ・エンドですか？

■ 解を振り返ってみます．

整数方程式「定石」のココロ

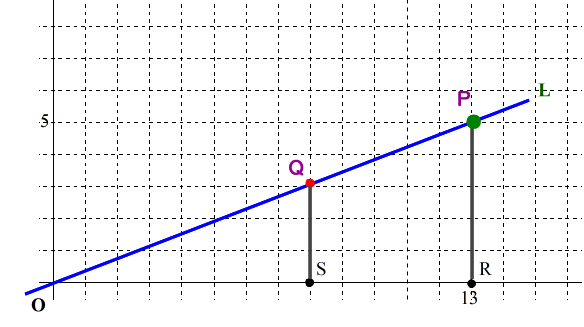
■ 整数方程式 5x-13y=1 の解は，直線L: y=5/13x-1/13 上で, x,y ともに整数となる点P(x,y)で表示されます．⇒ 点Pを座標面における格子点と言います（ふすまの格子のイメージ）．

次は，直線Lのグラフですが，解となる格子点が見つかりますか(マスの1辺が2の長さなので見づらいかも)？     

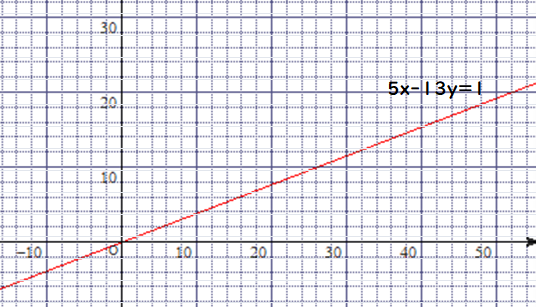
■ 点(8,3)や(-5,-2) など，確認できますか．

ところで，解答 A1 で，突然，①-② を計算しました．どんな意味のある操作だったのでしょうか．

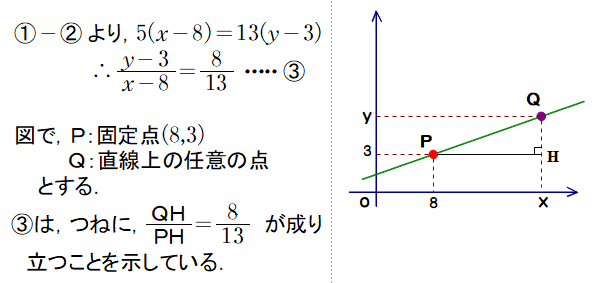
■ 何のことはない，相似比一定の性質(小6で登場)を導いているワケです．

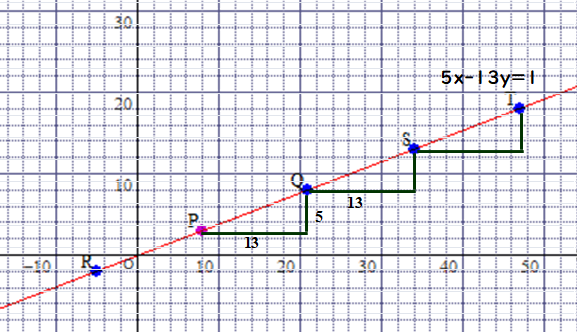
起点となる点Pを適当に一つ定めて，その後は，x軸方向に13,y軸方向に5 ずつ進める(後退も可)と，整数方程式 5x-13y=1 の解が次々と求められます．

■ 式操作①-② は，相似比一定を登場させるためのgood idea, いや, good job なのです．

互いに素：決定的条件

■ ”整数”にかかわると，よく 互いに素 という注釈がつきまといますね．実は，コレ，決定的条件になっていることがほとんどです．

Q2 先述の解説で「起点となる点Pを適当に一つ定めて，その後は，x軸方向に13,y軸方向に5 ずつ進めると･･･」ありますが，たとえば，2点(8.3), (21,8)を結ぶ直線上に，他の格子点はないのでしょうか．

A2 13と5 は，互いに素 ですから，直線上に他の格子点は存在しません．ワケは次のとおり．

’22共通テストの整数方程式問題････疑問？です

（以下，略）　

私見です．

■ (1)までは，係数に指数を用いた整数方程式ということで，少し興味がひかれましたが，次の(2)から「整数方程式はどこへ行ったのか？」と思うくらい力点がズレていきました．

■ 限られた時間の中で，マークシート特有の「作問者ideaストーリー」の把握・理解に努めつつ，その単純計算量には閉口しました（計算器使用不可）．

■ 本問は，示された指数係数の場合に，整数解がタマタマ求められた例であって，一般形に発展するような価値あるideaに基づく出題だったのでしょうか？

■ 数ⅠAの全国平均値38点未満(※)ということでしたが，さもありなんです．作問主メンバーは，他の大問も含め，全体を制限時間内で解いたのでしょうか？

※の結果 ⇒ マーク式宿命の偶然正解率(4択なら25％)と平均値がこれほど接近してしまうと,受験生の学力を適切に把握できませんね(努力して力を付けたヒトとそうでないヒトが同じ扱い！)．

■ 杞憂でしょうが，次年度以降，極端な「易化」に振れないよう，願います．思うに，マーク式で，記述式を上まわるような中身にするのは，仕組みからしてムリです(どうしてもゴールへの誘導が強くなるので)．学習の到達度を把握するための，「足切り的な役割」でもよいのでは．

＜補足＞

■ 整数方程式には，「解なし」もあります．4x+6y=3 などがその例です．

■ 次回のテーマは，「どっちが大きい？」です（予定）．大小比較は，数学の原点ではないかと思います．

■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(最初:左，次:右).