”無限”は小2で登場!
無数・無限は数学(or哲学)で扱う大テーマの一つです.算数・数学についていろいろと論を展開する際,無数や無限との出会いをどう扱っていますか?
■ 限りなく大きい(=無限大) の記号は,∞ と表され,高数Ⅲで登場します.
すると「17歳前後で無限を習う」のだという見解が示されそうですが,果たして正しいのでしょうか.
無限という語句は出ていませんが・・・
■ 無限の中には,「いくら数えても切りがない」という場合も含まれます.この視点から算数・数学の教科書を眺めてみます.

■ 教科書では,いくつかの例をあげた後「数を入れかえてもいいよね」と,サラリと交換法則を認めさせるストーリーとなっています.
■ ただ,いくら成立つ例を列挙しても,所詮,有限回です.そこから突然,すべての数の場合について交換法則の成立を示します.この論理の飛躍に多少なりともココロの痛みを感ずるべきかと思います.
価値あることとは
■ 小2生に語るかどうかは別にしても,学びのどこかの段階で次のような確認くらいはほしいところです.
5+5+5+5+5+5+5 = 7+7+7+7+7
よって,5×7=7×5
ワケは下の図で考えましょう.

上図で長方形の大きさを変えることにより,自然数における乗法の交換法則:ab=ba には繋がり,多少でも”ココロの痛み”は和らぎます.
定理や公式が成り立つプロセス軽視・無視は罪です.「答えさえ合えばいいんだろう」というヒトを増やします.教育基本法とまではいかなくとも,学習指導要領の精神に反すると言えます.
■ 要は
5×7=7×5=35 と答えられることは大切
しかし,“なぜ一致するのか”に関心を持ち,説明できることは,それ以上に価値あること です
まずは,公式の中に次の語句の挿入を提案します.

■ 図形の例をあげます.
定理 三角形で,3つの内角の和は 180° である.
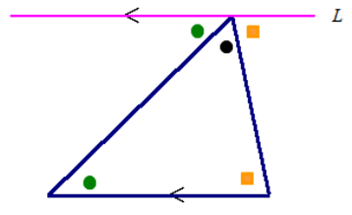
<略解>図のように,頂点を通って,底辺と平行な直線Lを引く.すると,2つの錯角の性質を用いると,3つの内角の和が一直線,すなわち,180°になることがわかる.
■ この解説(証明)に関連して,次の問を設定しました.
Q1 上図は,定理を鋭角三角形で解説しています.では,鈍角三角形の場合の解説はどうなるでしょうか.
① 要らない
② 鈍角三角形の場合は,再度図を描いて解説しなければならない
③ どちらとも言えない.鈍角三角形の形による.不要のときもあるし,再度描く必要のときもある.
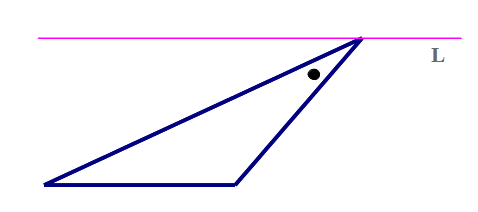
※ Q1は,当然正解は①ですが,全国学テ問題(’08 中数A)を参考にしたものです.
誤答が半数近いという結果には衝撃を受けましたね.
■ 「生徒が苦手とする証明の克服に努めてきたつもりだが,証明する意味自体が伝わっていなかった!」との悔恨の声が上がったものでした.
■ とりあえず,この定理も次のような表現に直すことを提案します.

Q2 「二つの奇数の和は,偶数になる理由を述べなさい.」という問について,次のような解答があります.正解でないときは,間違い箇所を指摘してください.
(1) 3+7=10, 15+9=24 などの例から明らかである.
(1)’ 全部やってみたらそうなった.
(2) nを自然数とすると,奇数は,2n-1 と置ける.したがって, (2n-1)+(2n-1)=4n-2 これは2の倍数だから偶数である.
(3) 3+7=10 ここで,10は偶数だから証明終.

<解説>
自分の周囲にはこんな解答をするヒトいないよ,と豪語する向きもありましょう.しかし,事態はそんなに甘くありません.
本問は「AI vs.教科書が読めない子どもたち」(新井紀子)を参考にしました.類似問題で大学入学直後の学生6000人の正答率は,34%だったとのことです.
(1) 成り立つ2例を挙げたに過ぎない.
(1)’ いくつか試した例をもって「全部」と主張していると思われる.
(2) 二つの奇数を共に2n-1 と置けば,同一の奇数となり,題意と合わない.
(3) どうやら文脈から 適合例を一つ挙げればよい と考えた節があります.つまり,ここで言う 二つの奇数 ⇒ 任意の2奇数を指すという理解がされておらず,数学用語(or日常用語)の解釈が正確でないと見るべきです.
数学を通して読解力向上に貢献する
■ ここで,学生の読解力不足をボヤイても仕方ありません.ボヤキは責任転嫁に繋がります.算数・数学を通して読解力向上に努める責任があります.
Q2 も以下のような補足説明を加えるなどして,まずは,題意をしっかり伝えることが基本になります.つまり,意味理解の徹底が改善の一歩です.

導入段階では,このくらいまで題意理解の徹底を図ることで,2奇数を 2m-1, 2n-1 (m,n は自然数)と置く・置ける背景が分かります.
⇒ 文字のよさ(ありがたさ)を感じさせることが,文字の活用に繋がります.
<補足>
■ SNS全盛期ですが,簡単に「いいね」と言わせないのが無限の世界.∞君!今こそ出番ですぞ.
■ プロセス重視の決定打は,テストに出題することです.指導者の本気度を子どもたちは分かります.プロセス理解を経て思考力を高める術が,昨今流行のストーリー性あるテスト形式にも対応可能かと.
■ 次回は,新学期早々ですので,数学に限定しないテーマになりますが,「”協議”は目的か手段か」(予定)です.アクティブラーニング精神よろしく,”協議”が大流行ですが・・・.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).