ナヌッ!?とくる問題

一瞬，ナヌッ！とくる問題ってありますね．twitter上で見かけた例やオリジナル問題から，いくつか紹介します．解く・解ける に留まらず，先に繋がることを期待します．

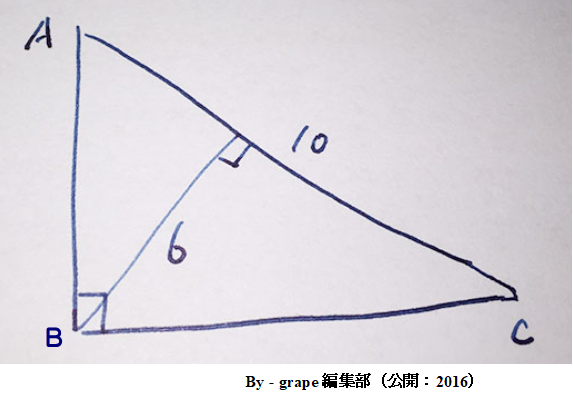
Ｑ1 下図で三角形ABCの面積を求めてください．

 

Ｑ2 次の問に答えてください．第30回富山県思考大会（小学生）より

 

Ｑ3 自然数{1,2･・･ 9} のうち，３つの数を用いてできる一番大きい数をかきなさい．同じ数をくり返して使用してもかまいません．

   

解答例

Ａ1 一説によると，本問はマイクロソフト社の入社試験で出題されたとか（未確認）．そんなこともあって”一世風靡”した問です．

　まず，△ABC=6×10÷2=30　は不正解です．

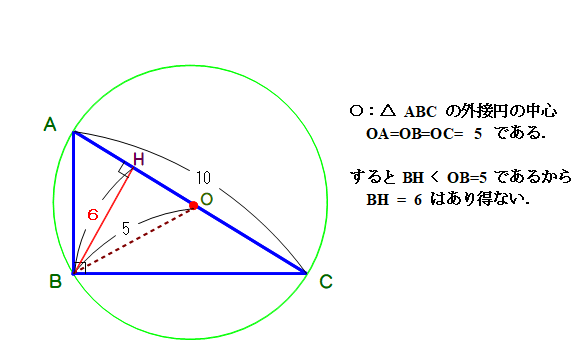
よって，本問は，出題にミスがあるので，「解なし」となる．

■ 外接円に気付けばよいのですが，ひらめかないときは次のような解説もあります．

＜別解＞

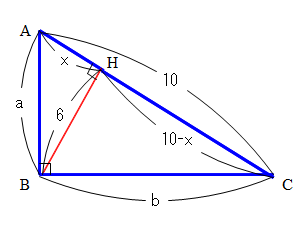
■ 次に紹介する解が出題側の意図に沿っている感じがします．

＜別解その２＞

命題 p ⇒ q において，仮定p: 偽のときは，結論q の真偽にかかわらず，命題は全体として真となる．

本題については，条件に合う三角形が存在しないため，仮定が偽ということなので，結論（面積）は，30をはじめどんな答えであっても，解全体としては「真」ということになる．

注意：命題論理式の背景を示さず，単に30と書かれている場合は，「０点」でしょうね．

 

Ａ2 白黒をそれぞれ数え上げて比較するのは，「最悪手」ですね．図のように，白黒同数ずつの適当なエリアに線を引き，最後に残ったエリアだけで大小を調べます．⇒ 黒が白より4個多い．

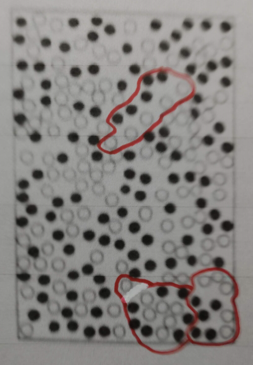
各エリア内で，１対１対応(one to one) の発想を活かしています．

1対1対応は，算数の植木算～代数学まで，重要な場面で登場します．基本の基となる数学的思考ですね．数も知らない原始人たちが，食料を分ける際に使用していたと想像され，数詞の出発点です．

 

Ａ3 999と答えた方おりませんか．たかが３桁ですよね．

高校数学までの範囲ならたぶん次の数ｙが最大値と考えます（とんでもない関数があったりすればおわびします）．

Ｑ3′ yはかなり大きい数となるが，一直線上に書くとする．その際，各数の間隔を1cmとすると，ｙはどのくらいの長さとなるか．

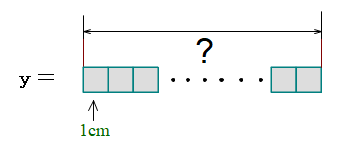
Ａ3′  9⁹ までならナントカ結果は求められます．

各桁の1数字を幅1cmで書き連ねますので，yは，

　少なくとも369676001cm≓3696760m≓3696.8km

 よって，yを書き連ねると少なくとも約3696kmの長さになります．

⇒ 北海道から沖縄までの直線距離は約2400km

 

＜補足＞

■ 富山思考大会ですが，60年以上の歴史があり，各問も実によく練られていると感服しております．継続は力なりですね．同県の理数教育が充実している背景が理解できます．

■ 次回テーマは「近似式の意義」（予定）です．「数学は答えが一つ ⇒ 近似値を軽視」となっていませんか？　この姿勢はソンです！

■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左，次:右).