判断推理 ⇒ 改良ベン図でサクサク
是非はともかく公務員への熱は高いものがあります.今年度の公務員試験(1次)もほぼ終了.既に次年度に向けた準備もスタートしています.
■ 高倍率ゆえに,1次はペーパーテストで志望者を絞るしかなく,いきおい問題自体の難易度も上がっています.
■ 中でも数的推理・判断推理と称される分野の結果が合否に大きく響いているようです(公務員に必要な資質かどうかは”?”ですが).
ここでは,判断推理に焦点を合わせて,数学的思考を深めましょう.
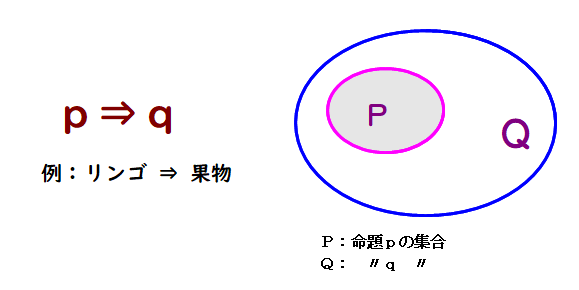
■ 上図のように,p⇒q と P⊂Q は同じ主張をしていますね(同値).
判断推理の一般的な解法としては,(1)三段論法(論理の流れを→で追う), (2)ベン図(集合による図解)による方法があげられます.
公務員対策用テキスト・参考書を見る限り(1)三段論法による解説が主流です(ほとんど).
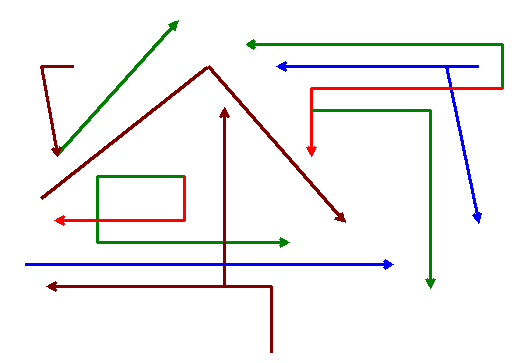
■ 論理式による解法は,多数の論理展開式の矢印オンパレードとなりがちで,”分かるヒトには分かる“という印象です.
■ しかし,論理で登場する定理・性質は,p⇒q のように集合のベン図で根拠を示すことが多く,したがって,当初からベン図によって解が求められるのであれば,単なる図形解釈になるので歓迎するヒトも少なくないはず.
判断推理の問題例
Q1 3つの条件があります.
a 赤いリンゴはあまい b あまくないリンゴは固い
c 大きいリンゴはあまくない

これらの条件から,確実にいえることはどれでしょうか.
①あまいリンゴは赤い
②赤いリンゴは大きい
③固いリンゴはあまくない
④赤いリンゴは大きくない
⑤大きくないリンゴはあまい
※ Q1の解説は後述
■ ここではベン図に”改良”を加えて図形解釈によるより原始的な解法に取り組んでみたいと思います.
ベン図の弱点
■ ベン図の弱点は,条件が多くて複雑な場合,ベン図が描きにくくなるという点にあります.実際,条件が4つ以上か{and, or, not} の使用がからんでくると,ベン図はタイヘンです.
次の例を順にベン図で表してみましょう.
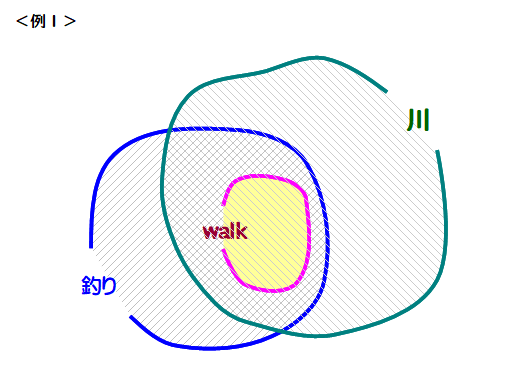
<例1> ウオーキングが好きな人は,川も釣りも好きである.
これは楽勝ですね.
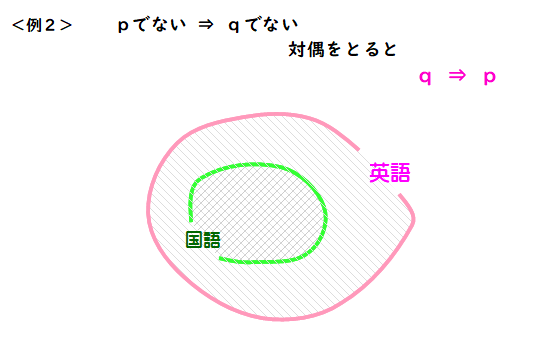
<例2> 英語が不得意な人は,国語が不得意である.
対偶をとるべき典型で,「国語:得意⇒ 英語:得意」となり,ベン図作成が一気に進みます.
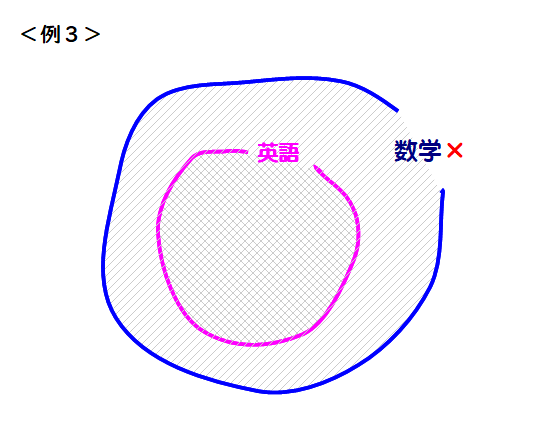
<例3>英語が得意な人は,数学が得意ではない.
対偶をとると「数学が得意 ⇒ 英語が不得意」となって,難易度においては原文と変わらず,堂々巡りとなり,ベン図作成も行き詰まりがちですね.
実際の公務員試験では,この”難易度堂々巡り”のケースが大半です.
ベン図を改良する
■ そこで,次のような「改良」をします.
数学が不得意 を1つの集合とみなし,ベン図にソノママ表します.
■ ベン図はもともと便宜的に描かれたもので,~A(=not A)はAの補集合,かつ, A∩(~A)=∅ ですから,~Aのベン図を上図のように描いても数学的に問題はありません.
<三段論法の”矢線恐怖症”の方へ>
要は,適切なベン図を速攻で描くことが出来るかどうかです.
ダメ元で改良ベン図による解法に挑戦してみてください.
3条件までの判断推理なら,この改良ベン図によりほぼ解くことができます(4条件でも何とかクリアできましたが,正直,シンドイです).
※ 改良ベン図は管理人オリジナルです(多分).三段論法の苦手者を念頭に,悪戦苦闘する中で考えつきました.
Q1 の問に戻ります.
3条件です.
a 赤いリンゴはあまい b あまくないリンゴは固い
c 大きいリンゴはあまくない
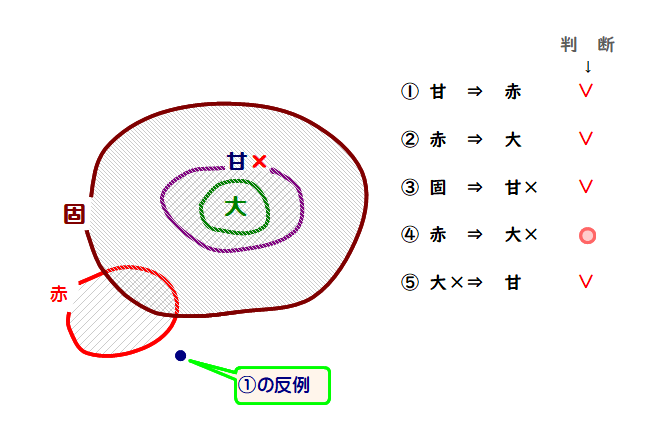
A1 改良ベン図は次のようになり,確実に読み取れる結論は④のみになります.
たとえば,①が成り立たない例(点)を●で示しました.
<補足>
■ 判断推理問題は,ハッキリ言えば「必要悪」かと(悪は言い過ぎか).しかし,現状を踏まえて,関係者の一助になればとの思いで書き連ねました.
■ 次回テーマは「~であることが知られている定理・性質の扱い」(予定)です.学習者の発達段階からその時点では証明しないで,結果だけ用いる定理ってありますよね.「良心」が痛みませんか?
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


