何のための式変形?
同類項をまとめる,平方完成する等々の式変形は,算数・数学の基礎であり,身に付くまでの反復(ドリル)も必要です.しかし「式変形のための式変形レッスン」のドツボにハマってしまうことも.

■ 式変形に限らず「学ぶ≓真似ぶ」ということで,ひたすら計算ドリルレッスンに没頭するとどうなりますか?
「思考する」ことよりも,「答が合う(マル○をもらえる)」ことに気持ちが傾きそうですね.
ここでは,学年進行とともに増加する式変形に焦点を絞ってみます.
式変形の背景を探る
■ もちろんドリルレッスンを否定はできませんが,学習者の”知的好奇心”を奪ってはいないだろうか,という警戒心は持ちたいものです.
(1) 同類項をまとめる

(2) 平方完成

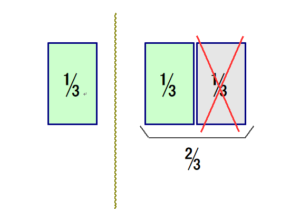
(3) 分数関数(仮分数→帯分数)

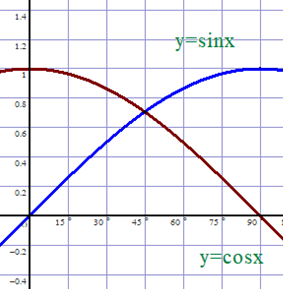
(4) 三角関数合成

数学的思考(発想・着想)を踏まえる!
■ 例1~4 は異なった式変形ですが,通底している思考があります.それは
単純化の考え
です.その具体の手続きが,同類項をまとめる,平方完成する,帯分数式にする,三角関数を合成する,となっています.
■ かつて菊池兵一氏は著書の中で
数学指導の中で,着想を明らかにしてそれを強調していくことは,学習者に
① 心理的安定感を持たせる
② 思考の面から系統性を持たせ,積極的に考えていこうとする態度の育成になる
と述べています.
<補足>
■ 本blogは「数学的な考え方を伸ばす指導」(菊池兵一)をベースに構成しました.同書はもはや「古典」に属していますが,中身は色あせておらず,むしろ「耳の痛い」解説が次々と述べられています.
■ 次回は新年ですので一般テーマとし「全国学テが語ること」(予定)です.
■ にほんブログ村のランキング(数学教育)にかかわって,バナーをclickしていだだければ幸いです.↓