今さら極限値ですが…

極限値ですが，計算は難しくありません．ただ「計算できるけど．知らんけど」という向きが多いのでは．

■ 教科書における極限値定義はおおよそ次のようです．

極限値定義の押さえどころ：３つ

■ 定義のpointは3つです．

① xはaにいくらでも近づく．しかし，aには到達しない

⇒ xがaとなった瞬間を不問（棚上げ）としたワケです

② 一定の値b とは，有限確定値：b という意味 

⇒ したがって，bが∞や±1（振動）となるときは，bは極限値ではない

　また，b=f(a) とあえてしていない点も注意（①より，x＝aは除外されているから）

③④ 波線箇所

⇒ つまり，「いくらでもbに近づく」というプロセス保証がなされれば，＝b とする大胆な決め方となります．2+3=5 の＝との違いがありますね．

同趣旨例：s=0.99999…  という級数は，いくらでも1に近づきます．

　　　　よって，0.99999…＝ 1 　です（とします）．

極限計算のそもそも

■ 極限の定義の解説後，即，前述のような実にカンタンな計算例から始まり，安心しているといかにも入試問題というレベルへと進みます．

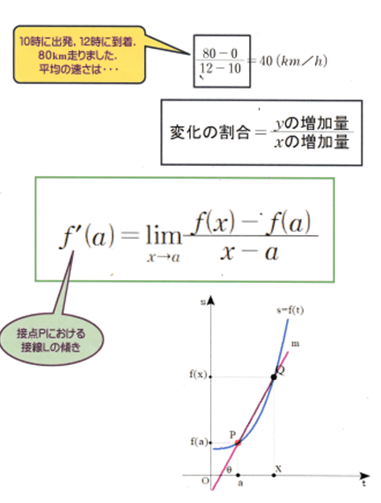
■ 上図のように，

平均の速さ（小6）⇒ 変化の割合（中3）⇒ 平均変化率・接線の傾き（高2）

と段取りを踏みます．

接線の傾きを求めるときに極限の概念を用いた（絞り出した）ワケです．

具体的には上図で

$x→a のとき，\frac{f(x)-f(a)}{x-a}\ (※)がどういう$

$値になっていくか(どんな値にすべきか)？ $

⇒ x=a の瞬間における※式の値を求めたい

しかし，単純に代入すると，※式は，0/0 ！ という結果になり，計算としては挫折します → “不定” とか “解なし” etc

「計算はできるが，中身は知らん！」をどう防ぐ

■ f(x)が連続関数の場合，極限値計算は，「xを限りなくaに近づけた結果」と「 x=aとして代入した結果」と一致します（例：x→2 のとき，x³→8 ）

この事実は「ごく自然・ごく当然」であり，多くの学習者に「当たり前感」が残りますが，学びとしては残念です．⇒ 「計算はできるが，中身は知らん」の原点

したがって，※のような不連続関数と向き合わざるを得ない接線の傾き（微分係数）をどう求めるか（どう定義するか）を徹底して問いかけ続ける必要があります．

次は，バカていねいに接線の傾きを求めた例です．

＜補足＞

■ 次回のテーマは「学習の進んだ子ども（その３）…1から1000まで書き続けた小1生」の続編です（予定）．

■ にほんブログ村のランキング（数学教育）にかかわって，バナーをclickしていだだければ幸いです．↓