学習の進んだ子ども
算数・数学教育に関わって「学習の進んだ子供」さんとどう向き合っていくか,はテーマの一つになります.基本的には,大歓迎で「喜び」「驚き」です.時には「戸惑う」こともあります.
ここで「学習の進んだ子供」の定義として,”テストで高得点を取る”が一般的には通用しそうですが,もっと広角で見てみましょう.
数年前,すごい少年を知る機会があり,心底,感激しました.
T君は,数を形に表しました!(見えた?)
算数・数学の自由研究コンクール(理数教育研究所主催)で,T君(九州地方の当時小6生)はテーマ「数を形に表す」で文部科学大臣賞を受賞しました.
T君の発表原稿の一部を紹介します.

T君の作ったルールは次のとおり.
- 分数を小数展開する(例:1/7=0.1428571・・・)
- 方眼紙上のある点(格子点)をスタートとする
- 小数点以下の数に対して,右→下→左→上(以下繰り返し)の向きに各数の大きさだけ進む
- 1/7の例:右1,下4,左2,上8,右5・・・
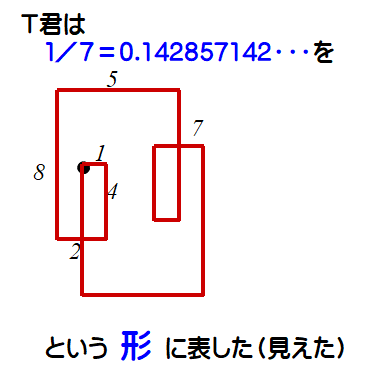
T君は,他の分数についても同じルールを当てはめてそれらの「形」を調べ,分類しています.
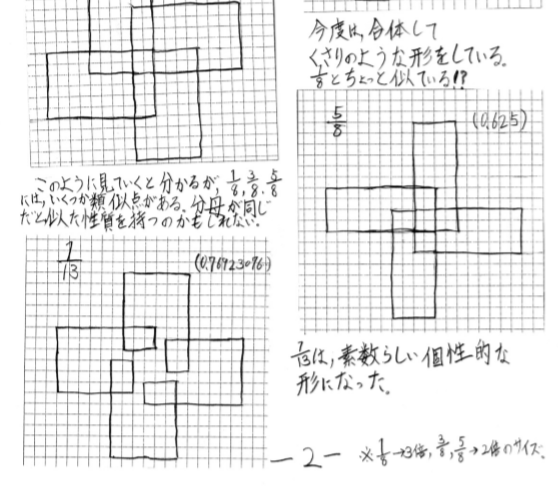
1/13については,「個性的な形」と言い表しています(確かに納得がいきますね).
作業してみると分かるのですが,1/3=0.333・・・などは正方形になって,グルグル回るだけですので,あまり「個性的」ではないですね.T君の発表は後半部分もありますので,関心ある方はネットで確認できます.
T君のマトメから
「・・・何の役に立つのか,と問われるとちょっと困ってしまう.しかし,美しい不思議を感じないだろうか.・・・ 数持つ性質を棒暗記するのではなく,身体で理解することが大切ではないだろうか」
とT君は述べています.こういう「感性」にこそ価値を置き,「見逃さない」でいきたいものです.
自由研究は,「問題を解く」に限定しておらず,いわば青天井です.スーパーchildrenとの出会いを大切にしたいものですね.
後で理解したことですが,最初に挙げた1/7は,実に「格好な」分数でした(1/7以外ですと,シンプル過ぎか,複雑過ぎ).
この種のコンテストで文部科学大臣賞にたどり着くまでは,通常,学校・県・地区・中央といった各段階での審査をクリアする必要がありましょう.
その中で,一番最初が要になります.「学校の授業で1/7がどんな数かを説明しなければならなくなった」とT君は説明しました.この点に注目しましょう.
担当の先生が,①「きっかけ」となる授業を計画実施したこと ②T君の発表内容に高い価値(評価)を与えたこと
この2点がなければ,当然,最後のゴールはなかった訳ですので,指導者「冥利に尽きる」し,やや冷静に言えば,教師の役割・使命を感じ入った次第です(担当の先生に敬服します).
T君に触発されて,問を考えました
有理数(分数)を小数で表すと,①有限小数,②無限循環小数 のいずれかになります.
Q1 T君ルールに基づくと,無限循環小数は,1/7や1/13のように,必ず閉じた形(いつか出発点に戻り,後は同じルートをたどる)になりますか?つまり.形が発散するような例はありませんか?
Q2 座標平面の格子点を考えます(格子点:x,y座標とも整数).出発点を原点(0,0)とします.点(10,10)をとおる分数を示してください.
<追加問> 円周率:π=3.1415・・・は,無理数ですから,循環しない無限小数となります.各位の数にT君ルールを適用し,出発点を原点とします.また,直線が各格子点をとおることを「πがとおる」といいます.
Q3 ある数のときに直線が原点(0,0)に戻ったと仮定(※)します.その上で,
(1) πが点(5,5) をとおることはありますか.あるとしたら原点を通過したときからそこまでの小数部分を示してください.
(2) 「すべての格子点をπはとおる」といえますか.
← 仮定(※)の確認もまだできておりません(しばしお時間を).解答をお待ち(期待)します.

<追記>
■ 次回テーマは,「”折る”操作:折り紙は深い!」(仮題)です.
折り紙は英語でもorigamiです.日本文化の一つですね.数理的な視点で教材化しましょう.
■ にほんブログ村のバナーをClickしていただければ幸いです(最初:右,次:左).



学園町1-1の住人です。共感します。ご紹介いただいたような児童生徒は、先生に恵まれてきたのではないでしょうか。彼の広角な発想を否定することなく、受容的な関わってくれていたのではないでしょうか。教師はともすると、指導方針や指導への信念が強くミスリードしてしまいます。また、自身の数学観の狭さも足引っ張りになります。この後の記事を楽しみにしております。
<住人様>
ありがとうございました.共感いただいたことに,重ねて共感させていただきます.
教育の語源がeducationで,「引き出す」とあります.すると,教育関係者は,①全員の子供を一律にある水準まで引き上げる,②それぞれの子供が持っている能力をそれぞれ引き上げる という義務を負っていると考えます.
①は学力保証の観点,②は個別の成長保証の観点 と言えます.特に,②については,非常に「心配」です.引き上げる前に「引き出す」センスが大人には求められていると思ってきました.スポーツや文化芸術の世界では実現されているようですが・・・.