学習の進んだ子供 part2

■ 算数・数学教育に関わる者（シャ）にとって，子供の伸びは大きな喜びです．

■ また「学習の進んだ子供」の”才”との出会いも，感激・驚きです．

■ その際，”才”については，ややもすれば”テスト高得点”に目が奪われがちですが，子供の学校数学を超えた”理数センス”により関心を抱き，それらの見逃し・見落としがないようにしたいものです（自戒を込めて）．

自由研究は「青天井」です

■ △△ピックや○○コンテストと異なり，自由研究は，正にテーマは自由ですから，正解があるかどうかも分かりません．既視感のある月並みな結論になることもしばしば．しかし，ゴールは 青天井 ですので，時に，目が覚めるような作品とも出会えます．

■ 算数・数学の自由研究コンクール（理数教育研究所主催）に応募した，Ｏ君（秋田大附中2年）の作品を紹介します．

■ 本作品は残念ながら入賞まで届かなかったのですが，私どもシャにとって，「なるほど！」「いいとこ突くな～」「これはツカえるぞ」等々の思いが発せられると確信し，本人・保護者・学校の了解を得て，ここに取りあげるものです．

素数が無限あることの証明･･･通常の解釈

■ 素数がヒトビトを惹きつける魅力は今も昔（大昔）も変わりません．中でも「素数が無限にある」という主張は，結論がシンプルであることに加えて，その証明の仕方も「いかにも数学」らしく印象的です．

■ いくつかの証明法が知られています．歴史があり，かつ，有名なのがユークリッド（古代ギリシア人．紀元前3世紀頃）による証明です．

■ 上記証明ではいくつかのpointがあります．

①（赤線部分）突然Pという数が登場します．そして，このＰが素数であり，かつ，ｎ個以外の新たな素数であることを示します．これは仮定に反するので，背理法によって，素数は有限個でない，つまり，無限個存在するということが証明がされたわけです．

しかし，どこかスッキリしない．「そうだろう」と言われると，仕方なく”妥協理解”する生徒・学生が結構います．

② この証明で，少なからずのヒトは，

（赤線部分）Ｐは ”素数の積＋１” という人工的な作りをしていることもあり，文句なく「素数であろう」と思い込んでいるヒトが少なくありません．これは，誤認です．→ もし，そうであるならば，式Ｐは，素数を次々に生成していくワケですから，証明自体が不要！となります．

③ ところで，Ｏ君は，Ｐ=2･3･5･7･11･13+1=30031=59･509 という例を発見しました．

つまり，p1,p2,p3,･･･,pn が素数でも，Ｐ＝p1p2p3･･･pn＋１が素数になるとは限らないのです．

④ すると，「Ｐは素数になる」というユークリッドの証明自体が成り立たなくなります．

そこで，Ｏ君は，以下のような解説を展開します．

素数が無限あることの証明･･･O君の解説

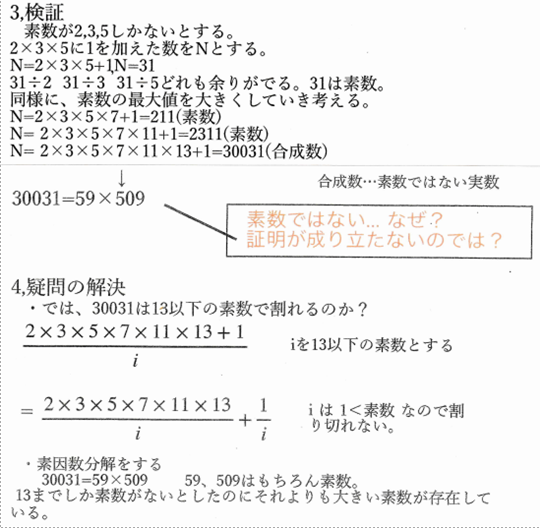
「Ｏ君解説」の解説

■ Ｏ君ストーリーの背景を推測します．

① n=1,2,3･･･と具体の場合から（→つまり，帰納的に），証明の意味全体の理解＆解釈をしようとしました．

② Ｐ=p1p2p3･･･pn＋１（※１）について，n=5 までは，新たなる素数を次々作る素数生成式として位置づけた感じです．が，n=6,つまり，P=30031 が合成数（59×509）であることに気付き，引っかかりを持ちます（→ 定理の説明との食い違い）

③ そこで，巧みな分数式：(2･3･5･7･11･13)/ｉ+1/ｉ を活用して，59(or 509)は2～13 以外の素数であることを確認し，このように，Ｐが合成数となる場合は，より大きい素数が存在であろう（※２）．

④ 以上のことから（※１）式は，素数生成式となり，素数は無限に存在することになります．

残った課題と補足

■ 上記（※２）部分の解説が30031の一例で終わっていますので，一般の場合の説明が必要です．→ 途中使用した巧みな分数式の適用でクリアできる気がします．

■ ユークリッドの証明方法についてですが，nは（Ｏ君が取り組んだような）帰納的に次第に増やすという発想ではなく，はるか彼方の大きな n（定数）という設定であり，そもそも否定される運命の有限仮定ですから，30031のような例外も出現します（→ 出現するのは，仮定が間違っているから！という，やや堂々巡りの感じもする論理ですね）．つまり，Ｐ式が素数であるかどうかには触れず，「素数が有限個である」ことのみを仮定した背理法ということなのです．