「攻める」復習を!
■ 復習とは”一度学習したことを再度勉強すること”,”おさらい”という意味で,十分理解している子供にとっては,不要でしょう.したがって復習から受けるイメージは,どちらかといえば,”後ろ向き”かも.

■ 授業では既習事項の確認(復習)をしながら本時の展開に入ることはフツーです.が,本稿では,補充や居残り,時には追試対策など,やらされ感のある”強制”学習の復習に焦点を合わせます.
復習・・・前に習った方法を”なぞる”のはやめたい
■ 学習者の立場で言えば,これまで習った方法では理解が十分でなかったワケです.したがって,復習を実施する際,これまでと同じような方法で,同じような説明を行うことには反対です.

■ 学習者からは「また分からないかも」「またすぐ忘れるさ」といった声なき声(怨嗟)が聞こえてきます.つまり,彼らの心理・心情を理解した上で指導方法に大胆な改善を図る必要があります.少なくとも導入の切り口に新鮮味がないと,無意識のうちに学びへの諦めが増幅され,結局,算数&数学と指導者への不信が高まりかねません.
■ 例で考えてみましょう.
割合(百分率:%)の復習
■ 割合(%)は小5で習い,小6では全体を1とする考え方が示されます(%の発展).
■ 次のような「復習」はいかがでしょうか.
Ⅰ % の量を「つかみ」で理解する
Ⅱ その後,計算作業に入る
Ⅲ この先に習うことに「少し」挑戦する
Ⅰ「つかみ」の理解
■ 適当な長さの板棒か物差しを用意します.Ⅱで計算するために,目盛りを付けた状態にした方がよいでしょう.
①「50%の長さまで塗りつぶしてください.ハイOKです」「次に75%は?」「半分の半分ということですね.ハイOKです」
②「30%はどうですか?」「少し足りない感じですね.左の50%と比べてみて.もう少し上」「ハイOKです」
→ このように「つかみ」で量(長さ)が測れるよう,10問以上(例:38%や15%・・・)は繰り返すべき.この授業だけでなく,日常の中で,機会あるごとに確認していきたいものです.
③ 逆に,長さを与えておいて割合(%)の見当を付ける訓練もしましょう.やはり10問以上は問い続けましょう.
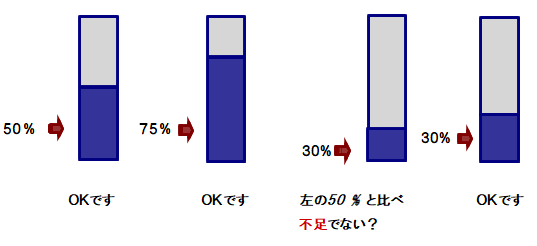
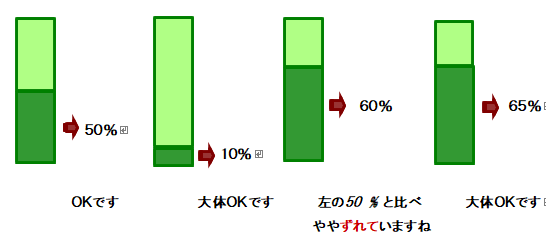
■ 量 → 数値(%),数値(%)→ 量 の対応がスムーズになるようにしたいもの.
割合%の数値計算については,おおよその%把握が出来ることが前提でなければなりません.つまり,まずは生活数理感覚を身に付けさせることを優先させるべきです.極論ですが,計算は機械に任せられます(しかもミスしません).しかし,結果として得られた数値の「妥当性」判断はヒトがするものであり,時には責任が伴います.
ある大学教官の話です.デザイン関係専攻の学生が,室内の天井の高さを10mとしてレポート提出したとのことで,「天井は吹き抜けなのか?」と問うても意味が分からずキョトンとしていたそうです.
Ⅱ 数値計算
略(教科書に準じて割合%の計算の仕方にふれる)
■ その際,結果について計算作業に入る前に「予想」させる習慣を身に付けさせたいもの.
■ 例:「70人のうち,55%は県外出身者で・・・」→ 県外出身者は35人以上いることになる・・・.
Ⅲ この先で習うこと への挑戦
■ 復習が「居残り強制」学習であった場合,参加しなかったヒトより何かしら「お得感」を持たせたいもの.
→ それには,”先の学習情報”が一番.
■ 次のようなニュースがしばしば報道されます.内閣支持率なども同じように扱われていますね.「500人にたずねました.この政策に賛成の人は60%,反対は30%,どちらでもないが10%でした.反対のうち女性は70%を占めています.反対の女性は何人でしょう?」
■ 割合が二重になっているだけの,数学としては単純な内容となりますが,実際にニュースを見てキチンと理解できる生徒・学生がどれくらいいるか,となると「怖くて問えない」タイプの設問になります.
■ 「AI VS 教科書が読めない子どもたち」(新井紀子著)でも似たような,つまり,読解力に欠ける学生の例が紹介されています.
■ 割合の二重問題は,場合の数における積の法則,確率の乗法定理と同じ本質を持っていますので,格好の予習材料となります.
分母の有理化の復習
■ ”分母の有理化”は,中3,高1で習いますが,単なる「同値な式変形」くらいのイメージを与えている感じはないでしょうか?「問題のための問題」という扱いです.残念! 微積分(特に積分)では,決定的場面でクリーンヒットを打つ感じなんですが.

■ 中3段階でも,有理化によってどんな”御利益”があるのか,伝えないと,”問題のための問題”になってしまいます.
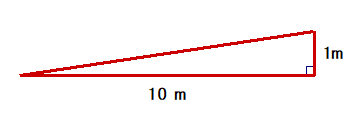
左図Q1で,単純な割算をする体験を通して,①と②が同じ値になるのはなぜか?という視点から有理化の意義を感じさせたいもの.
分子の有理化もあるのです・・・
■ Q2では,まず結果を見当付けましょう.d(差)は5cmですから,意外性もありますね.これまで学生に問たずねた経験では,5~10名で一人程度の正解「接近率」でした.
■ 分子の有理化は,将来,積分計算で力を発揮します.すなわち,「先の学習」です.大いに強調しましょう.
■ 分数の分からない高校生(昨今では,大学生も!)と向き合ってきました.だからといって,分数の復習をソノママ行うのはほとんど効果はなく,「自己満足」に近いですね.
■ 積分計算を紹介(理屈抜きで)して,実質は分数計算の場面を設定する,という実践もあります.