筆算の「舞台裏」
いまさら筆算?という声もありましょうが,筆算ルール・仕組みの大もとを確認することはムダではないと思います.

■ 筆算が”how to指導”に傾く事情は分かるのですが,徹頭徹尾ドリルで押し続けるのはいかがかと感じます.
■ 筆算に限らず,計算の原理を確認しておくことは, 直接子どもたちに説明する・しないは別にして,十分意味があります.
①指導上の余裕にもつながること
②指導者の”姿勢&奥行き”を見抜く子どもへの対応(小学生でも結構います)
10進法のつくりの確認
■ 一例として,かけ算 s =123×21 で考えてみましょう.
123と21 は10進法表記ですから,s=(1・10²+2・10+3)×(2・10+1) と書き表せます.
したがって,10の代わりにxを用いた次の多項式の展開と構造は同じです.

ここで,xや+記号を省き,係数だけ抜き出すと,右図のような筆算が登場するワケですね.
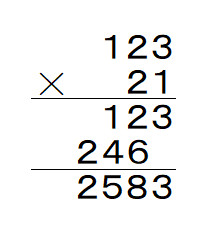
繰り上がりはなぜ起こる?
■ 上記のような例だけなら実にラクです.つまり(このあと話題にする)繰り上がりのないケースですから.
ところが,筆算で上下の段を加える(or 引く)際,困ることもあります.


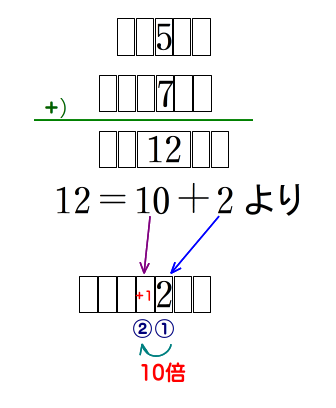
■ 図で,10進法表記ですから,それぞれの位は右から順に10倍ずつの値を示します.
したがって,②の1 ⇔ ①の10
つまり,同じ数でも,②の数は①の数の10倍の値に相当します.
■ このように筆算で,ある位の上下2数を加えたとき,その和が2桁(10以上)になると,次の位に1を加えます.この操作を繰り上げ(carry-up)といいます.
逆の操作を繰り下げ(carry-down)といいます.
筆算の「要」

■ 例:1111円分の金額
同じ数1が4つ並んでいますが,位(くらい)により意味が異なります
この意味理解がpointです.
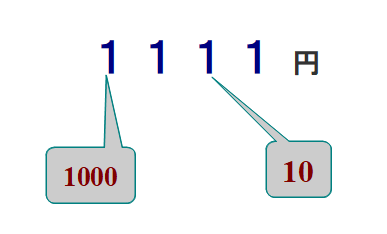
■ ほとんどの子どもは,金銭のヤリトリは日常生活の中で体験していると仮定してよいので,1111という数表示&量感(金銭感覚)にも抵抗はないはず.
⇒ 数学にとって日本の基本通貨(1円,10円,100円・・・)が10倍単位となっていることは実にラッキーです!
■ この「利点」を最大限活用しましょう.
10進法に結び付けられるかどうか
ペーパー上で操作できるかどうか
が到達評価の視点です.
⇒ 筆算は格好のペーパーレッスンになります.
■ このように
筆算の理解 ⇔ 10進法の仕組み理解
となります.
ただ,学習者の視点では,双方向というより
筆算レッスンを通して10進法を徹底理解する
と割り切ってもらった方がプラスになります.
<補足>
■ 次回テーマは「’22学テ公表から」です(予定).結果をいかに活かせるか,が最も重要だとは分かってはいますが…..
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).