”微分の源流”を算数にみる

「市民が学ぶべき数学のゴールは,微積分である」という声は,今や風前の灯火かも知れません.
ゴール設定が諸事情により困難であるにしても,到達ゴールをキチンと意識しながら,小→中→高→生涯学習へと進めたいものです.
一連の見通しの中で今をあつかう
一連の見通しの中で今を学ぶ・・・二つのkey wordがあります.”学力保証”と”知的刺激”です.
① 学力保証・・・教師の使命ですね
② 知的刺激・・・個々の子供の数理センスをキャッチし,より伸ばす.自身が彼らの成長の「踏み台」に.この姿勢が =信頼です.
2019年ノーベル化学賞を受賞した吉野彰氏の言葉は印象的です.
「きっかけは,小4のときに先生が薦めてくれた一冊の本「ロウソクの科学」(ファラデー)だった」

もちろん加減乗除を含め算数のすべてが“微分の源流”になり得るわけですが,ここでは,微分(の導入)と直結している算数の単元に注目しましょう.
それは,
- 単位あたりの量
- 速さ
- 比例
などです.この中で,「比例」に焦点を絞ります.
比例の延長線上に“微分”をみる
小6算数で「ともなって変わる2つの量」として比例(と反比例)を扱います.
例:バケツに毎秒1㍑ずつ水を入れたとき,水の重さは時間に比例する
ただ,比例を重視する余り,
「ともなって変わる2つの量」= 比例
という誤解を与えてはいけません.
どうすればよいでしょうか.
■ 「ともなって変わる2つの量」について,数理的観察力を豊かにすることが,まず重要です.急ぐあまり,即「比例」に帰着させるのは,×です.
■ 「これまでより2時間多く勉強したら,テストの点数が10点アップした.では,4時間増にしたら,20点アップしますか?」など.考える余地のある問いかけを準備したいもの.
■ このように,周囲をいろいろと見ると「比例関係にある2つの量」というのが,意外と少ないということがわかります.
■ 逆説的になりますが,「だからこそ,比例関係に気付き,かつ,計算式化できる」は意義あることになります.
■ 代表的な問を紹介しましょう.
Q 次の問に答えてください.← 小6算数で頻出(右図のグラフは中1数学)
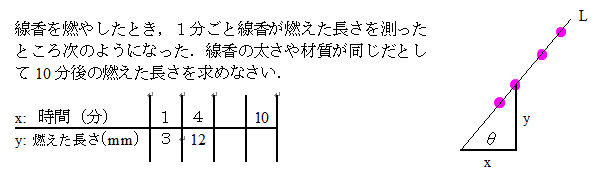
一次関数:y=ax は,やっぱり基本の基

■ マトメ:比例関係は,グラフでは直線(線分が多い)y=ax で示される.
逆の言い方も重要:直線は,比例関係 を示している
Q「これまでより2時間多く勉強したら,テストの点数が10点アップした.では,4時間増にしたら,20点アップしますか?」について
(1)単純に比例計算できない理由を挙げてください.
(2)単純に比例計算できる場合・場面を考えてください.
<解説>
(1)時間を掛けたからと入って,即,点数アップにつながるとは限らない.集中せず余計なことに注力すれば,逆にダウンすることも.
(2)それでも,勉強時間と成績は関係があり,一般的には,正の相関が期待できる.その前提で,保護者も教員も子供たちに助言することが多いわけである.
特に,計算問題や漢字書き取りなど,単純なドリル学習に絞れば,掛けた時間に見合ったマルをもらえそう.その部分に関しては,時間と点数は比例関係にあるといってもよい.

変化の中で,”比例部分”に注目する
この視点が,微分の idea につながっています.
■ 変化の中で,もっともシンプルなのが,比例です.
■ 複雑な変化の様子も,小さい部分にのみ着目すれば,比例と見なせる個所もあります.
■ 図形の中で,点の次にシンプルなのは,直線・線分です.
■ 複雑な変化を表すグラフは,増減や凹凸など,その姿はまちまちですが,ごく小さい部分に着目すれば,線分に近いことがわかります.
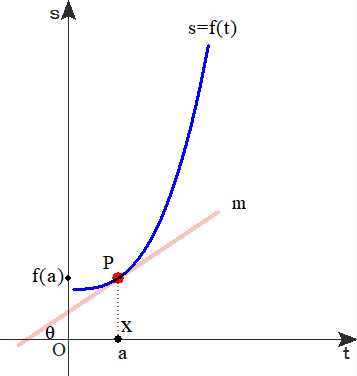
■ 上図で,点Pの付近で,tが大きくなるとsは増加しています.そこで,
①数式化,②増加の程度(急な増加か,ゆるやかな増加か) について考えましょう.
■ 先述した比例を使います.曲線全体の扱いは難しいが,tとsが比例関係になりそうな(直線になりそうな)個所に目を付けましょう.
点Pのごくごく近いところ(近傍という)では,曲線と接線m におけるsの値はほとんど変わらない.
→ Pの近傍では,曲線を接線mで代用できる
→ つまり,近傍における変化を比例とみなす
→ ①Pにおける接線mの傾き:微分係数といい,f'(a)とかく( f'(a)=tanθ ).
② f'(a)>0:右上がり,f'(a)<0:右下がり である(高校で習った増減表の根拠).
また,f'(a)の値が大きいほど,急な上がり方(or下がり方)となる.
例:f'(a)=1・・・接線mの傾きは45°
■ 最後に,曲線上の点の近傍における,
曲線≓接線 の様子を動画で紹介します(動画の扱いが不慣れですみません).
<追記>
■ 次回テーマは,「数学的思考は教え込まず,”なるほど感”で」(仮題)です.
分解や結合,逆向きに解くなど,数学的思考にはいろいろありますが,学習者自身が「気付く」ことに価値があります.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).