公式と「密」に!
■ 公式は論を進める際のツールで,活用により時間と思考の節約になります.
■ ガチガチに言えば
定理とは,証明された真なる命題
定理を数式で表したモノを公式
というようです.その外,近い表現として法則もあります.
■ これら公式等(以後,公式)は,論理と論理の間をつなげる場面で活躍します.
■ 中には,数学=公式 と理解する向きもあり,さらに,公式=暗記 となると,数学=暗記 ですから,これは,ただ事ではなくなります.

↑ 科学誌「Newton」別冊
■ 実際,三角比で,sin120°=√3/2 など有名角の値をひたすら「棒暗記」する高校生や覚え方をプッシュする指導者・参考書も散見します.
事情は様々でしょうが,数学が「1789年=フランス革命」の暗記と同列になるのは悲劇です.
科学誌で特集号を組むくらい三角関数は,サイエンスにとって重要かつ必須なのです.それを「棒暗記」などとという扱いは・・・耐えられません.
■ 公式が本格的に登場するのは,中学数学からでしょう.三平方の定理が代表ですが,近々それに加えて二次方程式の解の公式が入ります(昭和時代への先祖返りか!?).
■ 本稿では
①公式化を薦めたい例(特に,小学校)
②公式を無意識・安易に使用してしまい,「敬意」が不足している例
③公式を知らないと「タイヘン!」という例
について話題を提供します.要は,公式の御利益(ありがたさ)の紹介&確認です.
公式化したらどうでしょうか

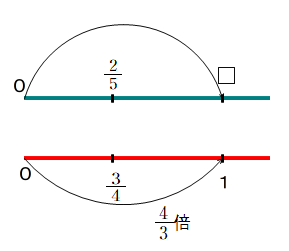
Q1 2/5㎡の壁を塗るのに,ペンキを3/4dL 使いました.このペンキ1dLでは何㎡の壁を塗れますか.(小5,小6算数)
A1 算数の中では手こずる領域の一つ.就職試験や適性検査等でも登場しますね.
式は以下のとおりです.
2/5 ÷ 3/4=8/15(㎡) ・・・①
①は1当たりの量,つまり,単位量の計算をしています.説明には数直線を用いることが大半ですが,学生にとっても結構手強く,計算は出来ても説明に苦しむ問となっています.
■ そこで,次のような「公式」を提案します.

■ pointは,a が整数だけでなく,分数・小数でも成り立つことです.なぜなら,計算結果が仮に○だとすれば,・・・○=○/1 と分母が1の分数形式となるからです.
Q2 市民のうち,地名変更に40%に相当する5500人が賛成しているという.市民は何人いるのでしょうか.
A2 単位量公式より,5500÷0.4=5500÷2/5=5500×5/2=13750(人)
■ 本公式について「抽象的で小学生がワカルわけない.数直線図で解くべき」という声もありましょうが,あえて公式化を提案します.
■ 就職試験対策(大半が中学校までの内容)で苦しむ高校生,学生,大人の”お寒い”実態を踏まえると,「単位量公式の記憶」を拠り所にして,学び直しをした方が現実的と考えます(適性検査等で大学での学びが問われることはほとんどありません.小中の算数数学が大半).
■ たとえば,解の公式の中身を忘れていても,その公式の名前自体が記憶にあれば,再チャレンジは可能です.本単位量公式(仮称)は,後々まで有効です.
公式を知らないと「大変」!
■ 公式や定理を最初に取りあげる際,「なるほど,これが公式のイミか!」と公式が公式たる所以をしっかりと押さえることがpointですね.意外性や驚きは意欲に直結します.
例を挙げます.剰余定理です.

■ 剰余定理については,その証明方法も独特であり,計算もわりと楽ですから,そんなに力(リキ)を入れることもなさそうですが,一事が万事です.もっと強烈に「なるほど感」を示したいものです.
剰余定理を知らないと,次のような計算を強いられることになります.実際の割り算を全部やれとは言いませんが,4段くらいまでは計算してもらいましょう.その苦労を身を以て知ることで,剰余定理の意義がシミジミと分かるのです.

※ 最後に余りは 8 となるはずですが,計算は長くなりそうですね.
公式の「無意識」「安直」利用
■ 公式や法則を無意識・無頓着に使用しているケースもあります.理由に一つに,使用している”記号のよさ”があります.記号が進行を促すような場合があります.
しかし,その”記号のよさ”に寄りかかり過ぎて(記号の巧みさにごまかされて),公式や法則の本質を見失ったとすれば,本人にとっても理数全体にとってもよろしくないことです.
例をあげましょう.数学の随所に登場する「線形性」という法則です. <参考>「高校数学の美しい物語」’15/11/19

■ 微分演算は,線形性の典型です.計算自体はラクですが・・・.

■ 線形性は,極限,積分,Σ計算,ベクトル演算,期待値等々,いろいろな場面で登場します.
例:Σ(k2+3k)=Σk2+3Σk=・・・
⇒ もしΣ記号に線形性が活用できなかったら,微積分は発展しなかったと考えます.
線形性は,小学校以来の比例計算,つまり,直線的変化の発展ですので,その単純性に思いを寄せながら学びを深めて行きましょう.
本blogのあちこちで強調してきましたが,小学校で習う比例&その考え方は数学の根底を形成しています.
<補足>
■ 次回テーマは「紙折りと指数」(予定)です.紙を折るという作業は,算数・数学の中でも代表的な操作活動です.指数に繋がっていきます.
■ 本ブログの冒頭(エンドにも)に,「にほんブログ村」のバナーが2つずつありますが,それぞかれClickしていただければ幸いです.



女子教育「コサイン教えて何になる」 鹿児島知事、撤回(朝日新聞 2015/8/28)
鹿児島県の伊藤祐一郎知事が、27日に開かれた県の総合教育会議で、女性の高校教育のあり方について、「高校でサイン、コサイン、タンジェントを教えて何になるのか」「それよりもう少し社会の事象とか植物の花や草の名前を教えた方がいいのかなあ」と述べていたことが分かった。知事は28日の定例記者会見で「口が滑った。女性を蔑視しようということではない」と発言を撤回する考えを示した。
総合教育会議での発言は、25日に公表された全国学力・学習状況調査の結果について、知事の目標設定を問われた場面だったという。知事は28日の記者会見で「サイン、コサイン、タンジェントの公式をみなさん覚えていますか。私もサイン、コサインを人生で1回使いました」と釈明した。
のことも思い出し、早速Newton別冊を注文しました。
ところで些細なことですが、Q1中の単位標記dlはdLが適切ではないでしょうか。個人的にはdℓと書きたくなるところですが。
考えさせられる話題を、いつも楽しみにしています。
「ご反応」に深謝いたします.自戒を込めて申しますが,昨今は,「発信」ばかりで「受信の巧みな方」が少数だと感じております.
本blogの中心は,「公式の無意識活用」と「三角関数(値)」でした.特に,後者に関しては,目にした少なからずの授業に「オヤオヤ・オイオイ」と思い,最近では,you tubeで評判の若手講師の画像を見てこれまたショックでした.両方とも棒暗記の仕方がメインの展開です.鹿児島県知事の件,記憶にあります(確か,”落選”したとか).暖簾に腕押しの感もありますが,これからも「話題提供」をしてまいります.予定では,5,15,25日にアップしてまいります.
※単位の件,ありがとうございました.教科書で確認いたしました.