身長と中間値の定理
中間値の定理を身近な例で再認識しましょう.ネーミングも気になります.マラソンで中間地点と言うように,”中間=真ん中” と受け取るヒト,いないのかな?
■ まず翻訳の件から.中間値の定理は,intermediate value theorem の訳なのですが,intermediate には,中間のほかに「~と~の間にある」という意味もあるのでよろしいワケ.
⇒ 実は,中間の第一義的意味は,「aとbの間」なのです(複数の事典より).したがって,中間値の定理は,適訳だったのです!
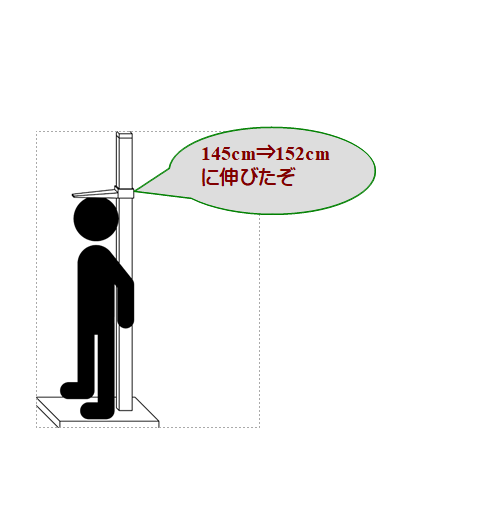
身長を測る親が語る
■ 小6男子がいます.身長がこの1年で145cmから152cmに伸びたそうで,親は喜んでいます.
■ 下図で縦軸はy:長さcmで,横軸はt:時間ですが,1目盛りを日から秒にします.
⇒ 1年=365日×24時間×60分×60秒=31536000秒
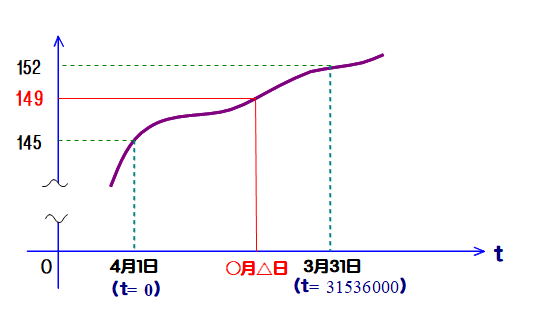
■ やや数学にうるさい親が言います.
「145cmと152cmの間の数なら何でもいいんだけど,たとえば149cmとする.149cmになった瞬間がこの1年の中であったんだよ」
「ヒトの身長は朝が一番大きいなど,1日の中でも多少の変化があるらしいから,149cmとなった瞬間は1回とは限らないけど,1回は必ずあった」
「その瞬間がいつだったかは分からないが必ず”あった”.ジャスト〇秒ではないときは小数で表すのだ」
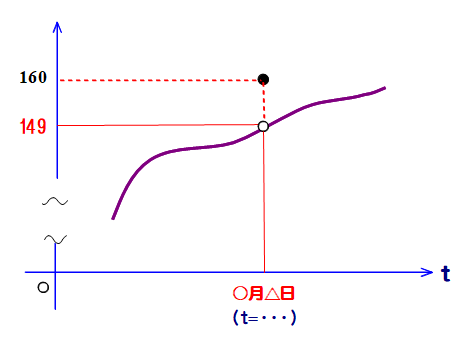
■ 時間tにおける身長をycmとして
y=f(t) と置きます(→成長曲線).
149cmの瞬間が必ずある とは ⇔ 149=f(t) を満たす t が存在する ということ
つまり,図のように,y=149 に対応する t がない! ということはない!! という意味
■ 平たく言うと,
y=f(t)のグラフは,突然,点がなかったり,点が「飛び地」になることはない
となります.
⇒ この性質を,曲線y=f(x) は,すべての点で連続である と言います.グラフが途切れることなく繋がっている というイメージですね.
■ また,一般に成長曲線は増加関数なのでしょうが,必ず増加状態が続くかと言えばそうではありません.
身長の場合も多少のアップダウンはくり返しますので,同じ数値をとるtは複数あり得ます.
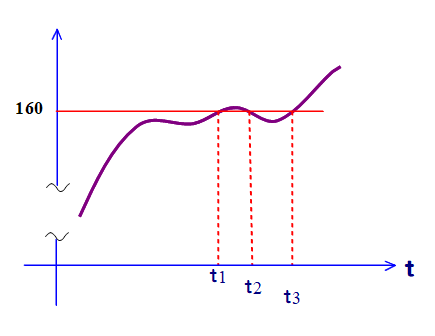
■ 上図では160cmとなった瞬間が,t1, t2, t3 の3回あったことと示しています.1日の中でも身長は多少伸び縮みするし,加齢により身長が縮まって160cmとなることもありですね.
くり返しますが160cmとなる瞬間は,必ず1回は存在する(ただ,いつだったかは別問題or不明).
以上,身長の話は,重要定理である中間値の定理の適用例でした.
中間値の定理とは


■ 核心部分は,連続性です.グラフが滑らか(微分可能)でなくてもよいのです.図のように尖っている箇所があっても構わない,連続=つながっている・途切れてない ことが必須条件なのです.
身長のケースで言えば
149cm となる瞬間(点)を飛び越して成長できない
という結論になります.
■ 本定理は存在を保証する定理で,その存在を明らかにする方法は述べていません.別途,考察が必要です.
⇒「この部屋にいる誰かが犯人だ.しかし,犯人特定については別に考えなければならない」
二次方程式 $ax^2+bx+c=0 $を満たすxは \[ x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \] で与えられます.例の二次方程式の解の公式ですが,解の存在とその求め方まで同時に示していますね.その意味で「公式」なのです.
<補足>
■ 「川を渡る」ときも中間値の定理が想起されます.つまり,「1時間前に川向こうにいたヒトは,この1時間内のどこかで川を横断したはず」.ただ,普通,横断箇所は橋と固定されてしまいますので身長測定に比べて面白みは半減です.
⇒ 「〇□川横断の定理」と名付けたいところ
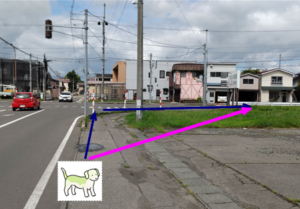
■ 次回テーマは「犬も最小値が分かる?」(予定)で,街で見かけた光景が発端です.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).