数学的思考は ”なるほど感”で
「主体的・対話的で深い学び」・・・私見ですが,欧米で見られる授業形態(思想)のいいとこ取りをするというイメージを持っています.この「いいとこ取り」の流れにまったく異論はありません.その一方で,教材自体への関心がきわめて低調である空気に危機感を覚える昨今です.ここでは中核となる数学的思考を取りあげます.
数学的思考とは

「数学的な見方・考え方」について.学習指導要領(算数)では,
「事象を,数量や図形及びそれらの関係などに着目して捉え,根拠を基に筋道を立てて考え,統合的・発展的に考えること」 とあります.
端的に言えば
前段・・・概念や法則等,数学的な”ことがら自体”(→知識),
後段・・・知識を基にした”着想や手続き” (→思考)
となりましょうか.
Q1三角形の内角の和は2直角(180°)であることを証明しなさい.
(→ 小5算数で話題に挙げ,証明は中2数学)
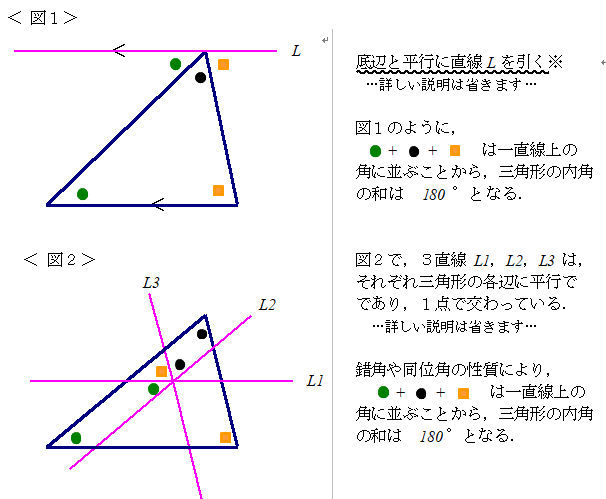
■ 教科書では,だいたい図1のような解説がなされています.
ポイントは,※部分:底辺と平行な直線Lを引く をどう捉えるか,です.
「ワザ」(How to)紹介だけ => 伸びる芽を摘んでいるかも
「ホラ,このように平行線を引いたら説明がつくでしょう」といったワザ紹介だけでスルーさせたら,生徒にとっては不幸!
■ 図2では,任意の点で交わる平行線を3本引いて,図1と同値の証明がなされています.
■ 3つの角の和が180°(一定値)であることの説明に対し
→ 3つの角を1個所にまとめる という発想(思考)まで昇華させましょう.
■ 本問から学ぶべきことは,解き方(how to)だけで終始することなく,基になる発想を”なるほど感”をもって理解し,身に付けることです.
(その結果,<図1>の場合が,一番簡単に済むケースであったという振り返りも)
■ ”3つの角を1個所にまとめる” 思考は,学習者が気付く・発見する形になればベストであることは言うまでもありません.指導者が焦る余り,早い段階で「解説」してしまう場面もよく見掛けます.
Q2 次は,3つの関数を変形したものです.これらの変形に共通する発想を述べてください.
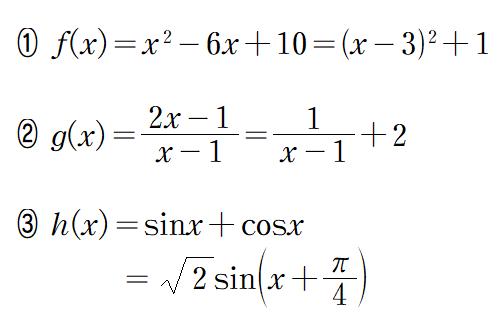
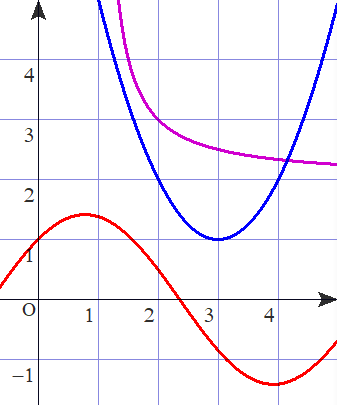
①:青色グラフ.2次関数を平方完成したもの.これにより頂点座標が(3,1)とわかる.
②:紫色グラフ.分数関数を帯分数に準じて変形したもの.これにより反比例のグラフ(y=1/x)を平行移動したものとわかる.
③:赤色グラフ.三角関数の合成による変形.これにより,sinxとcosxの和が,全体としてサインカーブとなることがわかる.
①②③の変形自体がさほど簡単ではなく,四苦八苦している生徒もいます.
- ①:1次係数の1/2を2乗して加えて,同じ数を引けばうまくいく
- ②:分数の筆算のように割り算をすれば何とかなる
- ③:三角関数の加法定理を巧妙に使うとよい
というような「ワザ」の披露だけですと,生徒には”なるほど感”は醸成されませんし,数学嫌いが増えるかも.
■ ①②③の左辺・右辺をじっくりと観察比較しましょう.
左辺:変数xは2個所に分散して存在している(例:②分母分子それぞれに)
右辺:どれもxは1個所に置かれている
■ この背景には 変数xは1個所にした方が,関数全体の変動を把握しやすい という発想があります.
<マトメ>
■ Q1,Q2を通して共通すること,それは,対象が図形であれ,数であれ,複数(個所)に存在しているときは,より少ない個所にまとめる・変形するという思考です.この思考は,別の場面でも活かせますね.
■ 本稿では,数学的思考の具体例を挙げました.このほかに,数学的思考としてより広義に,一般化・特殊化・類推・分解と結合などが知られています.”条件の一部を残して他を捨てよ”という大胆な切り口もあります.
<参考書籍等>「数学的な考え方と伸ばす指導」(菊池兵一),「いかにして問題をとくか」(Polya)
<追記>
■ 次回テーマは,「金銭感覚(その2)」です.(予定)
”「1万円借りても,利息は1日たった10円!」かつて,こんなコピーに惹かれ,借金返済に苦しんだ人が多くいました.自己責任でしょうが,学校教育の責任もありますよ(このコピーは今は使用されません.金利が法令違反だからです).
■ にほんブログ村のランキング(数学教育)にかかわって,バナーをclickしていだだければ幸いです.↓


