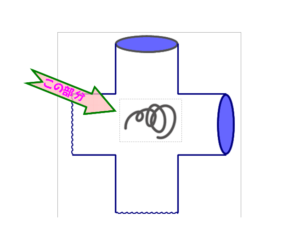
スッキリ感のない答え
数学の問題&解答について,「一応,頭では分かったというか,ナットクはしたのですが・・・.でも,正直,ピンとこないというか」.この種の声を耳にすることが少なくありません.今回は,私自身の体験をもとにいくつかご紹介します.
一応,理解はしましたが・・・の例
Q1 下図で,大円と小円は中心Oの同心円(小円はペンで描いたもの)です.大円を左側から地面に対して滑ることなく,時計回りに1回転して右側の位置まで移したとします.点P,P’はそれぞれの位置における接点,点QはOPと小円との交点,Q’はO’P’と小円との交点です.
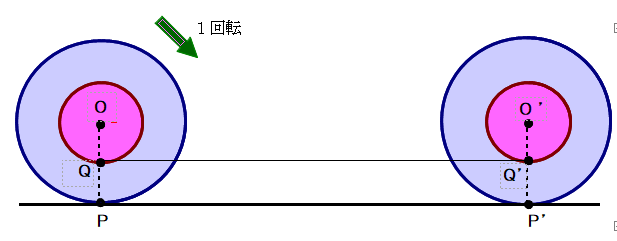
この図を見て妙なことに気付きます.
大円が1回転 → 大円の周の長さ=線分PP’の長さ
同様に
小円も1回転 → 小円の周の長さ=線分QQ’の長さ
当然,線分PP’の長さ=線分QQ’の長さ
小円は,大円上に描いた図ですから,空回りはしません.
したがって,大円と小円の周の長さは等しい!
また,小円の大きさは制限なしですので,極端な話,地球とピンポン球の周の長さも等しいことにもなります.
さて,どういう解説・解釈をいたしますか?
A1 解説(答)は以下のとおりです.かつて矢野健太郎氏(著名な数学者,数学教育者.故人)が,数学セミナー増刊号で示したと記憶していますが,今回,その増刊号を確認できませんでした.別冊子だったかも知れません.
<解>小円は,地面に対して,滑りながら1回転している.
<疑問点>前述したように,小円は,ペンで描いた図であり,いわば,大円と「くっついている」わけですね.その大円は,滑ることなく回転している.これは,どういうことでしょうか.思うに,小円は地面から離れているので「可能」となるのでしょう.でもイメージすることが難しくないでしょうか?
Q2 下図で△ABCは,AB=AC=1である直角二等辺三角形です(一般の三角形でもよいのですが話を簡単にするため).辺AB,AC,BCの中点をそれぞれM,N,A1とします(頂点Aを斜辺上に置く折り返しのイメージ).すると,AM=MA1,AN=NA1 となることは明らかでしょう.
つまり, BA+AC=BM+MA1+A1N+NC=2
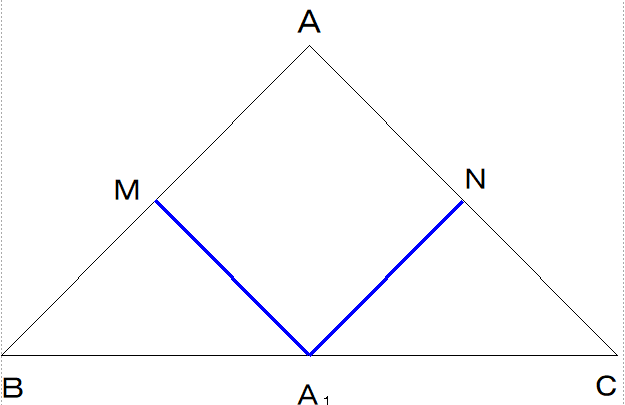
△MBA1と△NA1C はともに△ABCと相似の二等辺直角三角形となります.
そこで,△MBA1,△NA1C それぞれについて,△ABCと同じようにして頂点M,Nを斜辺上に置くように折り返します.
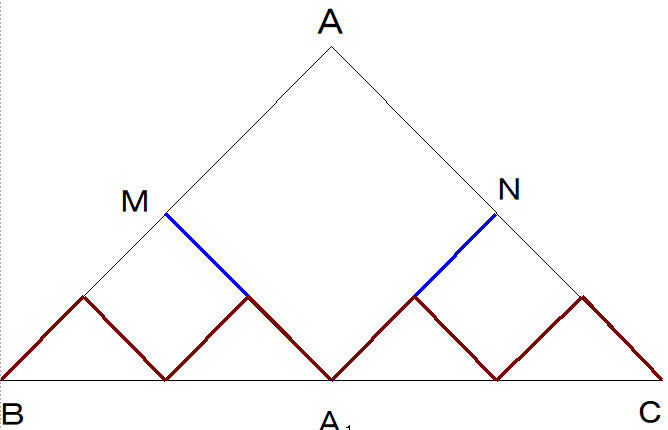
上図において,ジグザグ線(茶色)の長さ= BM+MA1+A1N+NC=BA+AC=2 となります.
以下,同じ操作を繰り返しますと
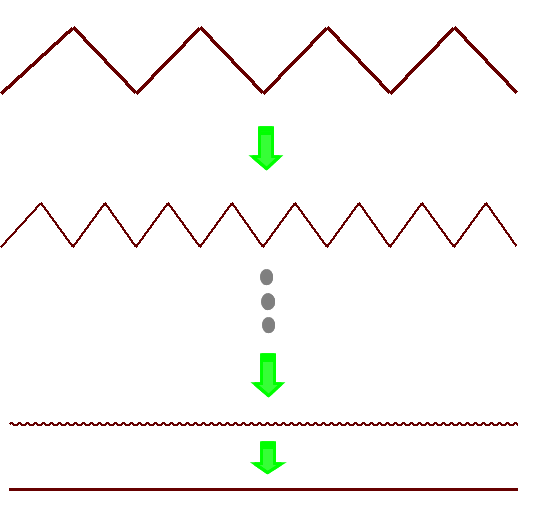
折り返しの回数をどんどん増やすと,ギザギザ線は,凹凸がより細かくなり,いくらでも線分BCに近づきます.
すると,究極的には(=極限値),線分BCの長さ(=√2)となりましょう.
ギザギザ線の長さは一定値(=2)ですから,2=√2=1.414・・・ これはおかしいですね.
A2 折り返し回数をnとすると,n→∞ のとき,ギザギザ線の長さ → 2(一定値)なので,極限値は2となります.ここまでの解釈は正しいと考えていますが,どなたか,線分BCの長さとの違いを説明できませんか.
ピリッとした説明であいまいさを吹き飛ばそう
■ 高校ではなじみの薄い分数関数についてですが,積分計算では重要な役割を果たします.分数関数には「部分分数に分ける」という独特の変形があります.
Q3 次の問とその解答を見てください.

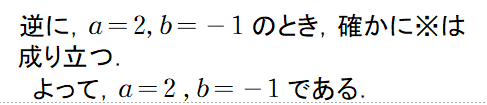
上の問で,※の恒等式は,当然ながら,xは1と2は除外されています(分母が0になるので).
ところが,略解の中では,x:任意の数ということで,堂々とx=1,2を代入して解を求めています(数値代入法).
除外された数を用いてもよい理由は何でしょうか?
A3 本問に関わる疑問については,いろいろな解説がされております.「数学迷答集」(BLUE BACKS)の説明が分かりやすい.
■ ※は,確かにx=1,2以外で成り立つ式です.
■ 分母を払うことで「※ ならば ①」は成り立ちます.
■ そこで,①を,xとして1,2を含めたすべての数で成り立つようにa, b を求める,とします.
以下,①にx=1,x=2 を代入すると,a, b が求まります(数値代入法といいます.この方法で得られた結果は,※が成り立つための必要条件であることから,逆:「a=2,b=-1 ならば ※」が成り立つ,つまり,十分条件であることも確認しなければなりません).

■ この解法で釈然としない理由があるとすれば何でしょう?
それは,※では,x=1,2 を除外していた(→ 仲間外れにしていた)
ところが,①においては,xは任意の数であることから,1,2も含めて①を見直します.たった今,”仲間に入れたばっかりの1,2を直ちに使った”という裁きがストンと落ちない理由でしょうか?
情緒面は別として,この裁きは,数学的にはまったく問題とならず,むしろ,スマートな方法となっていますね.
<追記>
■ 「スッキリしない問・解」はいくらでもあります.後日,再度取りあげます.
■ 次回テーマは,「立体図形」です(予定).円柱貫通体を取りあげます.立体が苦手な人,結構多いですよね.
■ 「にほんブログ村」のバナーがありますが,Clickしていただければ幸いです(最初:左).