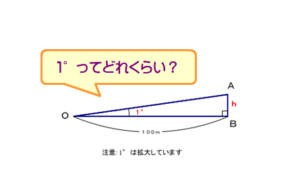
折り紙の”折る”を探る
折り紙は,英訳でもorigamiです.日本独特の文化と言えますね.今回は,「折る」という操作を数理的な視点で見てみましょう.
早速ですが,作業です.

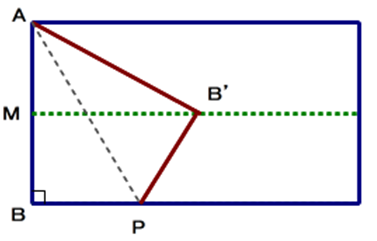

別解を一つ紹介します.
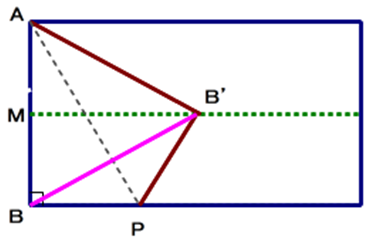

”折り返し”という操作(operation)は,線対称移動であり,合同変換の一つです.
上の証明から,その「要」を再確認しましょう.→ 「問題が解けりゃそれでいいでしょ!」はこれからの時代は×です.
折り返しの”要”
折り返しは合同変換ですから,図形の位置は変わります.変わらない(不変)モノは何でしょうか?
そうですね.辺の長さや角の大きさは不変です.
→ A君家族が,一家転住しました.住所は変わりますが,A君の身長や家族人数が変わらないということと同じですね.
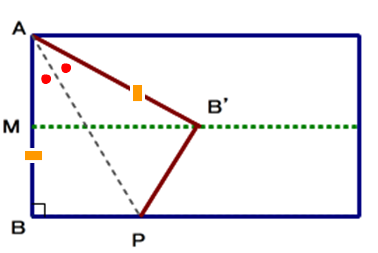
上記の解では,AB=AB’(辺の長さは不変),∠BAP=∠B’AP(角の大きさも不変)を明示できるかどうかが最大のポイントとなります.
「折り返しだから当たり前だろう」と感ずる向きも多々ありましょうが,実際はどうでしょう.本問の場合,中3生や高校生全般の正答率はどれくらい期待できますか? かなり厳しい結果を予想します(かつて教員採用試験で出題済み).
この 当たり前 感を取り上げます.次の画像を見てください.
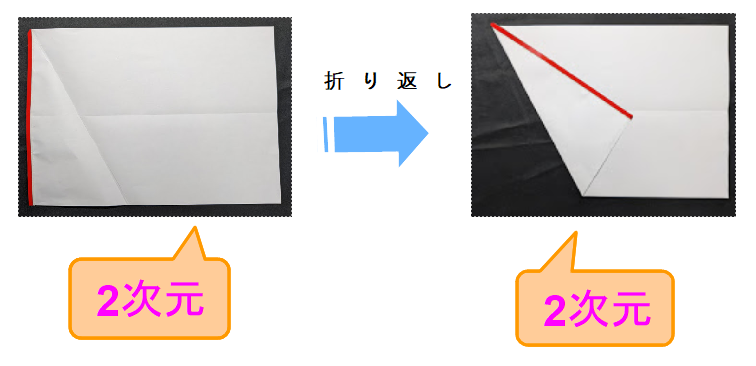
上図は,用紙の折り返し操作の前と後を表しています.共に平面ですから,2次元の図形になります.
赤い辺に着目すると,左図と右図で同じ長さであることは自明ですね.が,いざ証明の段となると,①気づかない,②なぜ同じ長さか分からない という子供が現れます.いるんですよ.そこで,移動途中の画像に注目しましょう.

この途中画像は,言うまでもなく,3次元図です.
- 左:2次元図の赤い辺
- 中:3次元図の浮き出た赤い辺
- 右:2次元図の赤い辺
ある2次元量を,一旦,3次元図で確認して,最後は,2次元量として再認識すること.
つまり,このプロセスこそが「折る」という操作の,中心的「目の付け所」ですね.
一般化しますと,量感覚を豊かにするため,
(n+1)次元に立って,n次元を見る
大切な思考だと考えます.
例えば,グラフや表を活用して速さ等の変化を理解する
→ グラフや表は「2次元」で,速さは「1次元」 という解釈も
具体の展開場面では,「移動で変わるモノは何?変わらないモノは何?」と操作途中の折り紙に注視させましょう.
また,各種入試(高校,大学)では,線対称移動に絡んだ問題がしばしば出題されます.
→ 反応は2とおり:①シメタ!,②ヤダー!
さいごは,念頭操作へ
当ブロブの目的の一つは,数理的「イメージ力の向上」です.
したがって,「折る」作業も,最後は念頭で行えるようにしたいものです.
→ つい各自の能力論に帰着させがちですが,その克服のため実践を豊かにしてまいりましょう.
補足

■ 折り紙自体が算数・数学(教育)の研究テーマになっているのは知ったのは,「折り紙と数学」(遠山啓序・堀井洋子著,明治図書)と出会ったときです.”折り紙で長方形を奇数等分する方法”など,興味ある解説が盛り沢山です(偶数等分は楽勝ですね).
なお,同書は現在,絶版ですが,復刻版を期しての動きもあるようです.
■ 問:正方形の各辺に頂点を置く正三角形(S)があります.Sが最大値をとるとき,Sを折り出してください.
<追記>
■ 次回テーマは,「算数に見る”微分の源流”」(仮題)です.
一市民(国民)の「数学ゴール」として,微積分を挙げる方が結構いるのではと思います.いかがでしょうか.
その視点から改めて算数を見てみます.
■ 「にほんブログ村」のバナーがありますが,Clickしていただければ幸いです(最初:左, 次:右).