“ねじれの位置”の数値化
空間において2直線がねじれの位置にあることを特殊なケースとして受け止めているヒトが少なくありません.はたしてそうでしょうか.そこで数値化を試みました.

ねじれの位置とは
中1の後半で学習します.

※1の説明文だけですと「何言ってるか分からない」「イメージがわかない」というヒトが多いと思われます.中1という発達段階からするとムリもない話かと.
そこで

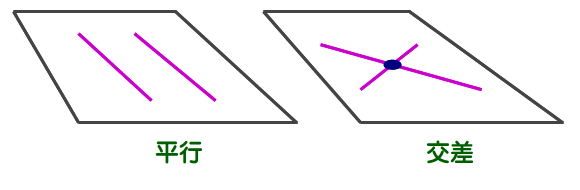
※2は 2直線が同一平面上にある・乗っかっている を示していますね.
したがって,2直線がねじれの位置にある その否定ですから 2直線が,同一平面上にない となり,図のような様子になります.
身近では“道路の立体交差線”に見られますね(直線部分).
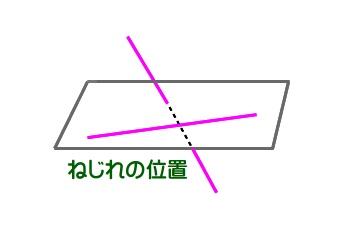

2直線が一致する場合も”平行”の一部とみなせば,空間内の2直線は次のようにまとめられます.
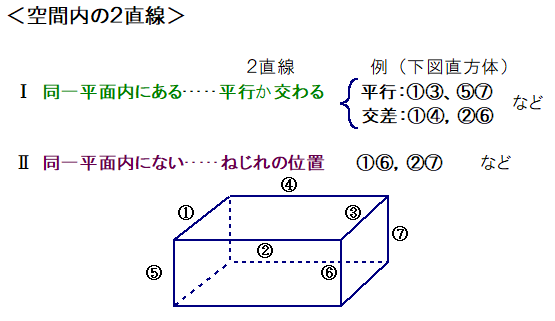
ここまでの説明ですと,空間内の2直線について,主役は”同一平面上の2直線”という印象を抱きませんか?
実際,上記直方体では,辺の総数12本から選んだ2直線の場合の数のうち,ねじれの位置にある場合は1/3(←同じものを含む順列として計算),また,問題集や入試問題で登場するのは”同一平面上2直線”がほとんどです.
しかし,空間には無数の要素(辺)があり,そこから任意に2辺を選ぶと,”同一平面上2直線”はどの程度出現するのでしょうか?
ねじれの位置の数値化を試みる
空間内に直交座標軸を設定します.適当に4点ABCDを選び,それらが同一平面上にあるかどうかを調べましょう.参考にしたのは,次のサイト「高校数学の美しい物語」です.
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
空間には無数の点が含まれていますので,無限に広がる空間に制限をかけて立方体とします.また,立方体内の要素を格子点として,4点が「同一平面上に存在」する場合をカウントして数値化を図りましょう.
そこで,図のような1辺100の立方体を想定し,その中の格子点に着目します.
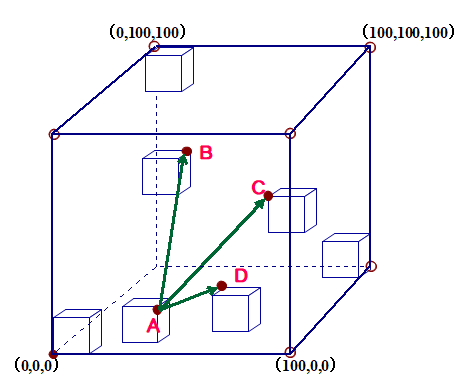

V内の格子点P(x,y,z)について,excel の random関数機能を用いて,x,y,z を 0以上100未満の任意の整数 として選びます.そして,その都度,行列式の値を瞬間的に求めていきます.行列式の値は,3ベクトルで作られる平行6面体の体積(符号付)を示します.
したがって,行列式=0 は,”つぶれた6面体”を示すということ.つまり,
行列式の値=0 ⇒ 4点が同一平面上にある となります.
Q 4点を100万個から次々とrandomに選んでいきます.その際,行列式=0 となる,つまり,4点が同一平面上にある となる出現率はどれくらいでしょう.
{①30% ②20% ③15% ④10% ⑤5% ⑥1% ⑦0% }
次の表は,乱数を発生して出現率を確認したexcel表の一部です.← <補足>参照
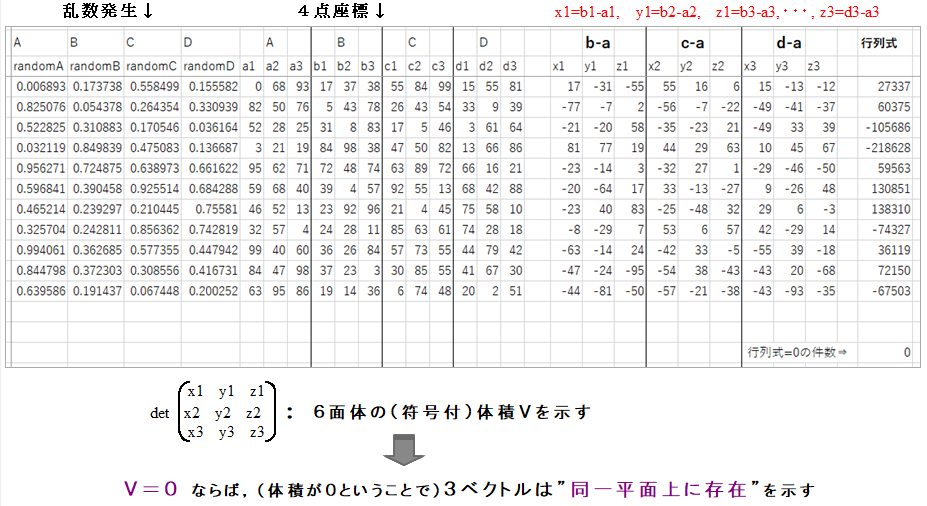
ねじれの位置の出現率
A 乱数を発生させることにより,ABCD各点のxyz座標にそれぞれ2000とおり(組)の整数値を当て,上記のように行列式を計算した結果,行列式=0 となったのは,わずか1組でした.すなわち,1/2000=0.05%です.99.95%の確率で4点ABCDは同一平面上にはありません.正解は⑦0%です.
このように,空間内の4点を任意に選ぶとき,その4点が同一平面上に存在することは,統計的には「ごくまれ」と言えましょう.つまり,ほとんどの場合,ねじれの位置になります.
※なお,立方体の1辺を10にして,格子点の総数を103=1000 にして乱数を1000とおり発生させたときは,1000のうち20回,すなわち,2% の出現率でした.
なぜ”ねじれの位置”と言うのか?
たとえば長方形の場合,一般の四角形が(無数に)ある中で,平行四辺形があり,さらに長方形がその一部としてある・・・こういう流れや包含関係を理解できるワケです.
比べて,”空間内2直線”については,包含関係のない ①同一平面上に存在,②同一平面上にない=ねじれの位置 と2つに大別するまではよいとしても,①のみに偏った指導展開が目に余ります.テストに出題しやすいから①を”偏愛する”,という見方も成り立ちそうですね.
結局,”空間内2直線”の指導展開を通して,ヒトビトの空間認識力は向上せず,むしろ,ミスリードしているとさえ感じます.無意識・適当に空間内に2直線を描けば,それは,まず,ねじれの位置になる,というイメージを持ちたい・持たせたいものです.
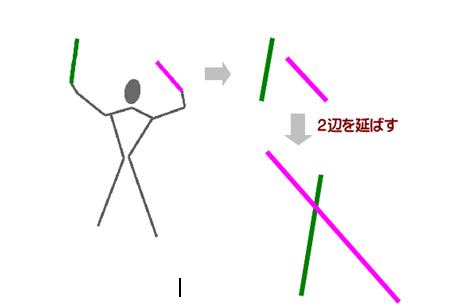
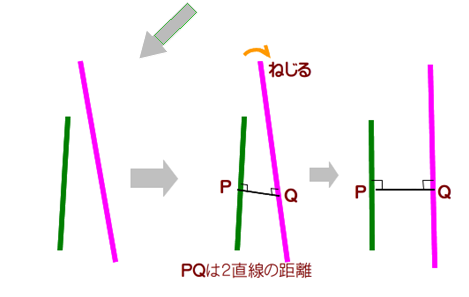
線分PQが2直線と垂直であるときに最小値をとりますが,その値を2直線間の距離といいます(証明は難しくありません).距離PQを軸としてどちらかの直線をねじる(or ひねる)と平行線になります.逆に,平行線1本をねじると平行線でない形ができるので,ねじれの位置 と命名したと理解できますね.
<補足>
■ ”ねじれの位置”は,中1(13歳)のときだけの取りあげになっています.もう少し取り上げる場面設定があるべきかと.教科書会社への希望です.スマホ画面でいくら工夫しても所詮2次元表示です.空間認識力はそれでもって身に付くほど甘くありません.
※excelの乱数発生についてですが,関数が進歩しており,本稿ももっとラクに出来たはず(昔のアタマ!).
■ 次回テーマは,「面積を測る」(予定)です.距離や重さを測定するグッズはいろいろ市販されています.しかし,面積測定器となると,ハードルは極めて高くなります.そこで,ささやかな代替案を・・・.
■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(はじめに左, 次に右).


