背理法とモヤモヤ感
背理法ですが,まず,漢字表記から受けるイメージがよろしくありません.何しろ「理に背く」ですからね.実際,多くのヒトにとって,背理法との初対面の印象は,どこかごまかされたような,スッキリ感の持てない出会いとなっているようです.

さらに,背理法に首をかしげていると,数学を得意としているヒトからは「数学論理の素晴らしさにカンドーする」みたいな言い方をされることもあるようで,背理法を巡って、教室は2分されるかもしれません.
源流は算数に
背理法の源流を算数に見出すことができます.たとえば,割り算です.
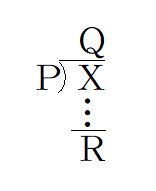
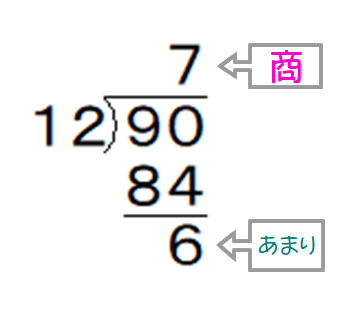
Q ある数XをPで割ると,商Q,余りがRでした.このとき,必ず R<P となります.イコールも付きません.なぜでしょう.
一般式では,X=PQ+R(0≦R<P) ※ となります.
A もし,R≧P としましょう.
つまり,余りRが,割る数Pと等しいか,または大きい ということです.
すると,割り算が終了していない!ことになります.
これはおかしいですね.原因をさかのぼって探ると,R≧P としたことにあります.
よって,余りは割る数より必ず小さくなります.
なお,※ X=PQ+R(0≦R<P) ですが,数学基本公式の一つです.剰余定理・因数定理と直結し,代数学の土台をしっかりと支えています.
”たかが余り,されど余り”です.
背理法とは
背理法の定義には微妙な違いがありますが,あっさり形を紹介します.
あることがらが成り立たないと仮定して矛盾を導くことにより,そのことがらが成り立つことを証明する方法
例1 自然数nがあり,n2が偶数ならば,nは必ず偶数である.
証明:nが奇数と仮定する.このとき, n=2k+1(k=0,1,2,3,・・・) と書き表せ, n2=4k2+4k+1 =4(k2+k)+1 となり,奇数となる.これは, n2が偶数という最初の条件と矛盾する.よって, nは偶数でなければならない.
例2 あみだくじでゴールが重ならないのはなぜでしょうか.(本blog ‘21.7.5「あみだくじ,重ならない?」再掲)
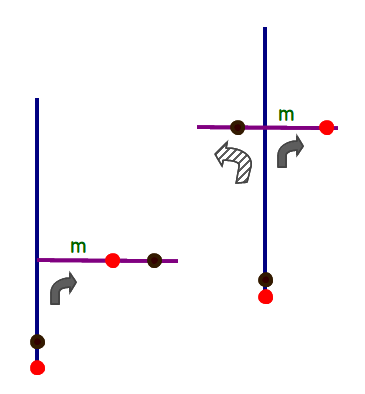
図(左)のように,別々の縦線をスタートした動点P1●, P2●が,同じゴールに着いたとします.P1,P2が通ってきたルートを逆向きにたどってみます.
直前に通過した横線mでは,ともに同じ向きからmに入って来ています(∵仮にP2が別向きから来たとすれば,図(右)のようにmは縦線と交わっていることになりますね).
さらにその前の横線でも同じことが言えます.以下,このくり返しで,最後は,動点P1, P2は同一の縦線からスタートしたことになり,これは,仮定に反します.
よって,P1, P2が重なってゴールすることはあり得ません.
以上の2例は比較的,ナットク感のもてる内容ではなかったでしょうか.次はどうですか.
√2:無理数の証明
背理法と言えば,「√2が無理数である」の証明が有名です.
※1 有理数・・・分数形で表せる数,無理数・・・有理数でない数
※2 近年,背理法によらない意外な証明も知られるようになりました.ご存じでしたか?
<証明の骨子>
① √2=q/p(既約分数)と仮定する(※既約分数と「p,qが互いに素」は同じ意味)
② 平方した後,倍数関係から,p,qがともに偶数であることが示される
③ この結果は,①の既約分数という仮定に反する
したがって,√2は有理数ではない.つまり,無理数である.

<モヤモヤ感>
(1) 有理数でなければ,無理数なのか?その他の数があってもよさそうな気がする.
(2) 勝手に既約分数と決めておいて,その些細な”既約”個所と合致しないからといって,仮定全体が否定されるのか?
(3) 直接証明ではなく,間接証明なので,どうしてもストンと墜ちない.ズルイ!という感じがしてならない.隔靴掻痒(靴の上から搔く)とはこのことだ.
モヤモヤ感1 ⇒ 排中律
排中律(ハイチュウリツ)は,基本論理法則の一つですが,背理法に対するモヤモヤ感の一つに,この排中律確認の”不徹底さ”があると考えています.
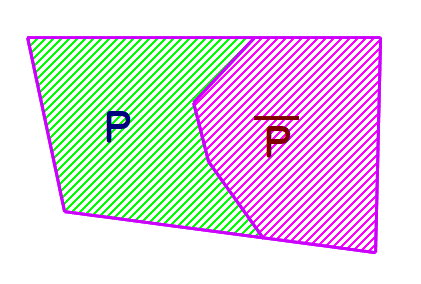
排中律とは,命題Pについて,
「Pであるか,非Pであるかのいずれかであり,その間はない」
という約束です.
(注)排中律を認めない論理もあるが,学校教育の数学は「認める」論理です.
刑事ドラマで,容疑者AとBが刑事に追い詰められました.ここで,Aのアリバイが証明されたとします.でも,即,Bが犯人だと断定されません.なぜでしょう.

ここが,日常と数学の世界が決定的に異なるところです.
まず,A,B以外に犯人がいないという証明は極めて困難です(極端な話,ウイルスだって犯人になり得るワケですから).また,Aのアリバイが証明されてもリモートで犯罪行為がなされる可能性もありましょう.
日常の中で「排中律」と出会うことはメッタにないのですが,すべてを単純化した数学の世界ではありふれた光景です.
「√2が無理数」の話に戻ります.
実数 a は,{有理数 か 有理数でないか}のいずれかで,排中律により,その間はありません.
そして,有理数でない数=無理数 でしたので
実数aは,{有理数 か 無理数} のどちらかとなります.⇒ ここがpoint!
ここで,√2 が無理数でない ,つまり,有理数であると仮定します.
(以降,略)
モヤモヤ感2 ⇒ 矛盾律
矛盾律も基本論理法則の一つです.
「Pであり,同時に,非Pである」ことはない
”Pであり,同時に,非Pである”・・・この個所を矛盾といいます.そして,ひとたび矛盾が示されると,それまでの論が矛盾律により否定されます.
<あみだくじの例>
ゴールで重なるとすれば,出発の段階から重なっていたワケで,これは,別々のくじを引いたことと矛盾します.よって,ゴールが重なることはない.
このように,矛盾が単純明快な場合はよいとして,論理が複雑で記述が長くなると,「これは矛盾だ!」と指摘されても,全体像の理解が及ばないことが,しばしばあります.
√2:無理数 ⇒ 再確認
第一に,√2は,無理数か有理数か,のいずれかであって,その他のケースが入る余地はない!ことを徹底しましょう.⇒ 排中律!
第二に,√2=q/p (既約分数)と仮定して,矛盾を示すのですが,その示し方に工夫が必要です.
計算を進めると,p,qが偶数であることが導かれ,これは,”既約分数”と仮定したことと矛盾する・・・・・モヤモヤ感の核心部分かと思っています.
実は,q/pが既約分数であるか,否かは,本質的ではありません.
既約としないで論を進めると,やはりp,q ともに偶数が示されますので,P=2P’, q=2q’ と置けます.それがくり返され p’,q’ が再び偶数となります.すると,偶数/偶数の形が永遠に続く・・・.そのような分数q/pは存在しませんので,背理法が成立します.
つまり,分数の既約性ではなく,「√2 を分数形式q/p と仮定する」こと自体が矛盾の大元なのです.
まずは「√2=q/p 」と仮定して,ドロ臭く論を進め,一応ナットクした上で,「√2=q/p (既約分数)」とすると,矛盾の示し方のスマートさが再認識できます.
多少,時間がかかっても,”背理法”を学習者の「敵に回さない」工夫を重ねたいものです.
<補足>
■ 次回テーマは,「意外な確率」(予定)です.確率も好き嫌いがハッキリしますね.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).