坂のθ(角)を測るヒトはまず「いません」

■ 量の中でその「量感」が比較的安定しているのは,長さ(1cm,1mなど)くらいでしょうか.重さや広さ,速さなどになると”迷う”ヒトが多くなりますね.
■ 中でも角(度)は,身近で扱う機会もほとんどなく,量感を持つのは大変です.
■ では,坂の勾配(傾き)についての量感をチェックしてみましょう.
Q1 図は,べた踏み坂で有名な江島大橋(えじまおおはし)です.この坂のθ(角度)はどれほどでしょうか?正解は最後に紹介します.
Q2 次の写真は,ある旅館で見た階段です.けっこう急で慎重に上り下りしました.さて,この階段のθは何度くらいでしょうか.


A2 30°少々です.いかがでしょうか.いろいろなヒトに問うと35°~45°という答えが多いです.中には,まったく声に詰まる,つまり,「角度なんて使ったことがない」というヒトビトも結構います.
Q3 次は,スノーボード・ビッグエア(2018平昌冬季オリンピック)と蔵王スキー場(横倉の壁)の様子です.これら斜面のθはどのくらいでしょう.

A3 急斜面のトップに立った経験ある方は分かりますよね,恐怖心で足がすくんでしまい,感覚としては「垂直に落ちる!」です.
でも,この急斜面も θ=38°~39° なのです.
同じような例を蔵王温泉スキー場(山形県)で見つけました.

雪で苦労しました・・・
Q4 次の画像は,この年末年始に経験した大雪「始末」の様子です.左のスコップの画像は,右画像の雪山(2F屋根からの落雪で積み上がった)のてっぺんから下を見下ろしたものです.この雪山のθはどのくらいでしょうか.

■ 遠近感がなく傾斜が分かりにくいですが,上下にあるスコップの大きさから坂の状態を想像してください.
数メートルの坂ですが,すべり落ちると下の用水路に突っ込みますので,けっこう怖いのです.

■ なお,雪山は放置しますと2F屋根と繋がってしまい,屋根に雪が溜まります.すると,大量の雪が一気に落ちるなど,かなり危険な状態になります.したがって,屋根と繋がらないよう,つねに,雪山を崩す作業が必要です.
A4 分度器で測ると, θ≓36° です.
■ 45°くらいという声が多く,このズレが約10°というのは無視できない数値だと思います.それも高校生や学生など,今現在,数学を学んでいる現役のヒトビトも含めての話です.
■ つまり,角に対する量感覚がかなり貧弱であることの証左ではないでしょうか.これは学生と接しての感想ですが,数学の得意・不得意とはあまり関係ないようです.
次に最近,経験したショッキングな例を紹介します.

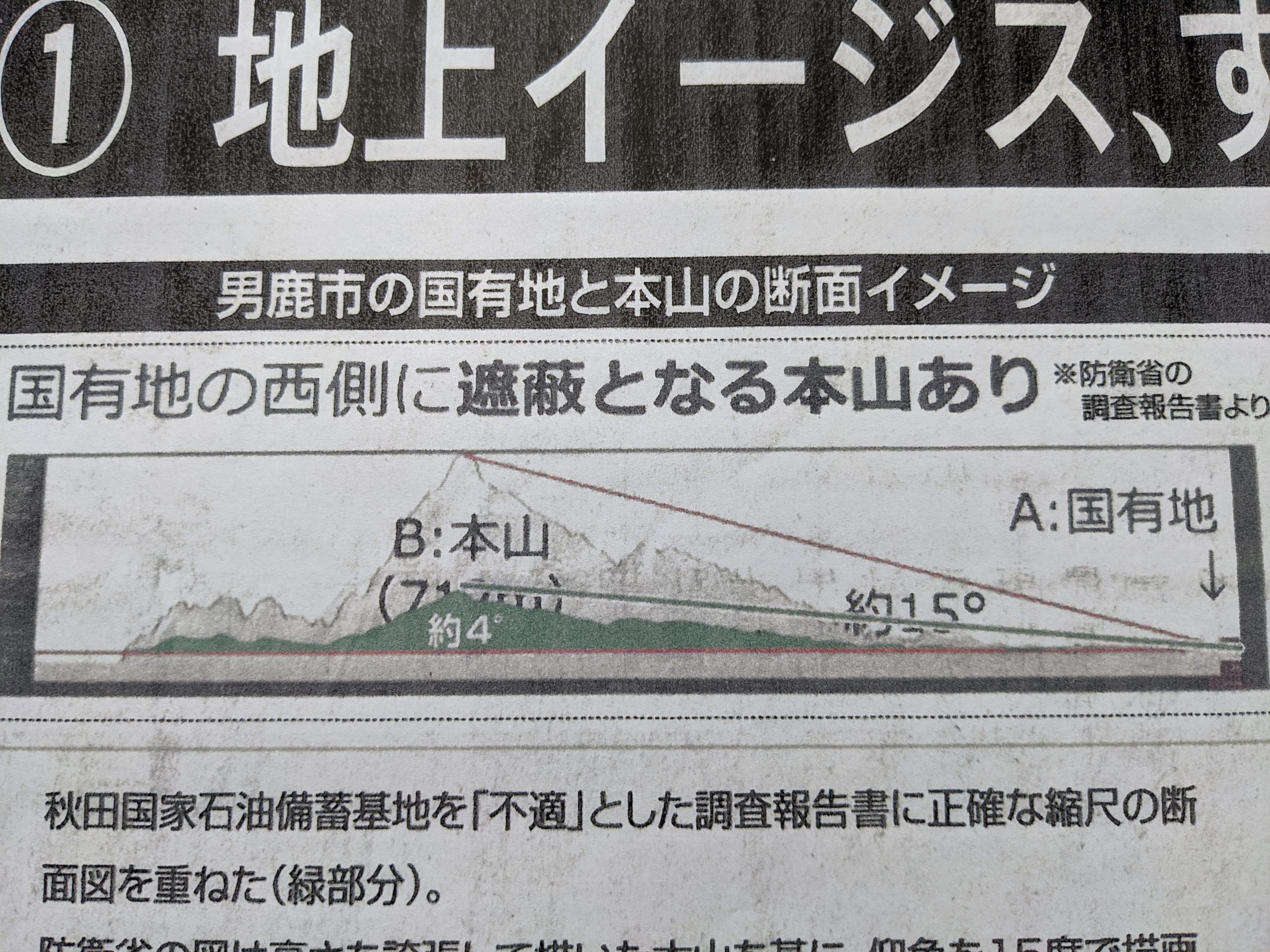
秋田魁新報記事より(’19新聞協会賞,’20菊池寛賞を受賞)
■ ご存じない方もいるでしょうが,イージス・アショア設置に関連して,その方向性を変更させるスクープ記事が地元紙(秋田魁)に掲載されました( ‘19.6).
ここではあくまで数学(算数)の視点から話題にあげます.
■ 国の報告書に,候補地の一つが不適という根拠について,「仰角が約15°になる山の存在がある」旨の指摘がありましたが,この数値自体,つまり核心部分が大きく間違っていた事実が報道されたのです(正しくは,4°).
■ このミスは,引用した断面図が横軸縦軸の尺度が異なっているのに同一と見なして分度器で測ってしまったというのが真相のようです.
■ あの地区に仰角が15°にもなるような山ってあるかな?という素朴な疑問が取材の出発点だったとのこと.
■ これまで紹介した例で分かるように,30°以上の斜面は急勾配です.
そのヒトのスキー技術にもよりますが,スキー場の斜面も,20°あたりからキツく,並のスキーヤーがまずまず滑走できるのは10数°くらいまでかと.
したがって,15°も結構な斜面なのです.低山の多い地区ではまず見られない勾配となります.
■ 計算能力とは,計算力+結果考察・判断する力ではないでしょうか.その際,量感覚の有無が極めて重要な要素となりそうですね.
算数における角の説明
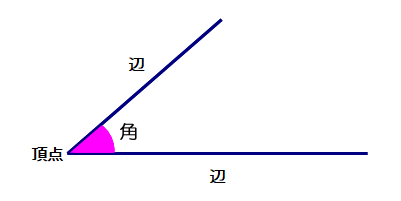
■ <小3> 図形の一つ として扱う
頂点から出ている2つの辺がつくる形を「角」といいます.
⇒ 図を見てください.角も図形の一つとして扱っています.
ただ,図形としての角は,2辺の開き具合ですから,頂点や辺と比べて,つかみ所がない感じですね.
角の認識が弱い原因の一つがここにありそうです.
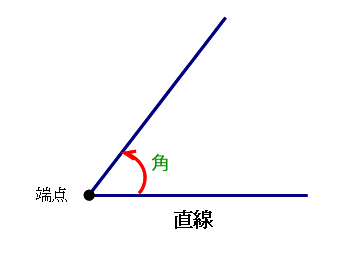
<小4> 回転量 として扱う
角とは,直線を,端点を中心に回転してできた形として扱う.分度器もこの視点でみると,作りの意図がよく分かりますね.
⇒ 角を回転量と見なすことで,三角比・三角関数に直結する
A1 江島大橋の θ についてです.国土交通省によると,勾配は6.1%, つまり,tanθ=0.061 ,したがって,θ=3.5°
45° などと思った方いませんか?実は,画像が望遠レンズで撮られているため,遠近感が極端になくなったため生じた思い違いです(マラソンのTV実況中継で,先頭集団がばらついているのに,正面からの映像画面では選手同士が近く見える光景と同じ).錯角,いや錯覚でしたね.
⇒ そもそも45°の坂を車(それも軽自)が登れるはずがありません(江島大橋が有名になったのは某社の軽自動車の宣伝からでした).
<まとめ>
■ 量としての「角認識」は極めて弱い.例えば,気温について10°も違いが出ることはまずない.しかし,角度の世界ではしばしば見られる.
■ 原因は
①長さや温度と比べて,日常的に数値を確認する機会がほとんどない(cf:気温は毎日,天気予報で取りあげられる)
②学校の数学では,30°,45°,60° それらの倍数という,いわゆる有名角を主に扱っている.理由は,入試等で出題されるからであろう.つまり,角は「問題のための量」と成り下がっている.しかも,その有名角は前後の角との比較がなされないため,その量感自体が不足するという悪循環に陥っている(⇒坂の勾配が50°などと,非現実的なことを答えてしまう).加えて,sin60°=√3/2 とは書くが,√3/2≓0.87 という認識に欠ける生徒・学生が多い.
■ 結局,三角関数をツールとして活用していく,ものづくりに関わるヒトや理工系学部学生(特に,工業実習のない普通高校出身)にとって,「角量認識」不足で戸惑うこと多々あるのではと推測する(国全体のマイナスも大きいはず).
■ 対策は,授業だけでなく,日常の中で角を認識する機会を意図的に増やすことに尽きる.坂など具体の事物⇒角を推測&測定,33°など具体の角度⇒事物を探す 等の地道な取り組みが大切.また,現実的には,テストに出題することで一層効果が増す.
■ 「1°」にこだわったblog(1°はどれくらい?)も参照してください.
<補足>
■ 次回テーマは「2/0.01 はなぜ重要か」(予定)です.分母がやたらと小さい分数計算があります.別にイジワルしているのではありません.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).