重心はなぜ一つか
重心をめぐるあれこれの話題は,かなり「スジ」のよい数学導入ツールになります!
重心とは
■ 物体の各部に働く重力をただ一つの力で代表させるとき,その作用点を重心Gといいます.(小学館デジタル大辞典による)
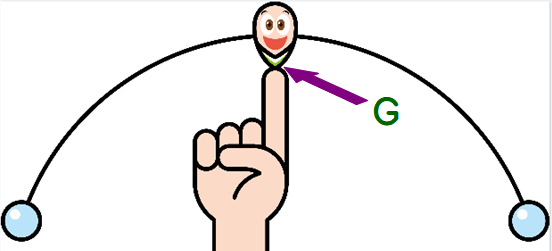
重心は一つ
■ 高校生や学生に「重心は一つしかない.なぜ?」と問うと,大半がキョトンとした表情をします.
「聞いたことがない」「聞かれたことがない」「考えたこともない」.中には「そんなことを考えてもテストに出ない」という反応も.
Q1 重心は一つのみ存在することを証明してください.
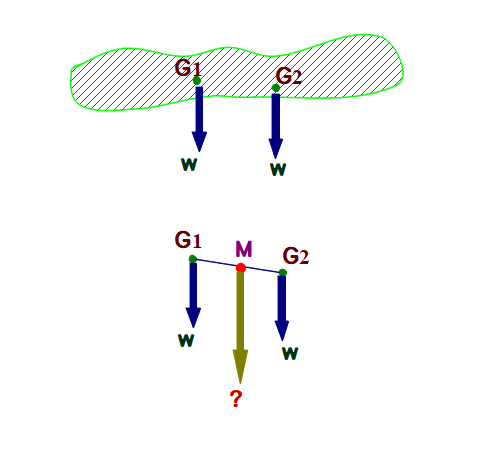
A1 (上図)ある物体の重心が2つあったとし,それらをG₁,G₂ とする.
物体の重さをWとすると,重心G₁,G₂において下向きの力がそれぞれWはたらいている.
(下図)G₁,G₂ の中点をMとすると,Mにおいて下向きの力がはたらいているが,その合力は2Wとなる.
これは物体の重さがWであることに反する.したがって,重心は一つしか存在しない.
重心と存在定理
■ 存在定理・・・中間値の定理&平均値の定理がその代表ですが,もう少しハードルを下げて適用例を示したいもの
※存在定理:数学的対象の存在は保証する定理のこと(求め方は問うてない).例:5次方程式には,代数学の基本定理より解が存在する(しかし,解の公式がないため,計算式で解を必ず求められるとは限らない).

■ 厚さは無視できる板状の物体Sがあります.Sの重心Gを求めましょう.
Q2 図のように,Sの端点でヒモを吊し,その鉛直線をL₁とします.
(1) SはL₁により左右S₁,S₂に分かれますが,それぞれの重さは等しくなることを説明してください.
(2) S全体の重心をGとします.GはL₁上にある(存在する)ことを説明してください.

A2
(1) ヒモで吊して静止したときの鉛直線がL₁であるが,S₁,S₂それぞれの重さが一致しないとすれば,L₁は静止せずに動くはず.よって,S₁,S₂の重さは等しい.
(2) S₁,S₂それぞれの重心をG₁,G₂とすると(1)の結果から
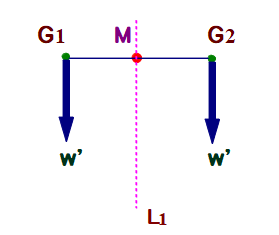
G₁,G₂にはたらく力(重さ)は等しい.
線分G₁G₂の中点をMとすると,S全体の重さがMにはたらいているので,MはS全体の重心Gである.
ヒモで吊してS全体が静止した ⇒ Mを作用点としてヒモで吊り上げバランスがとれた
つまり,Mは重心になる.重心は一つしかないので,M=G である.
したがって,重心Gは,ヒモの延長である鉛直線L₁上に存在する
(注) M=G より,Gは簡単に作図できそうだが,任意の図形でG₁とG₂を定めることは自明ではなく,この段階でいえることは,”重心Gは鉛直線L₁上に存在する“までです.
Q3 Sの重心Gを作図してください.
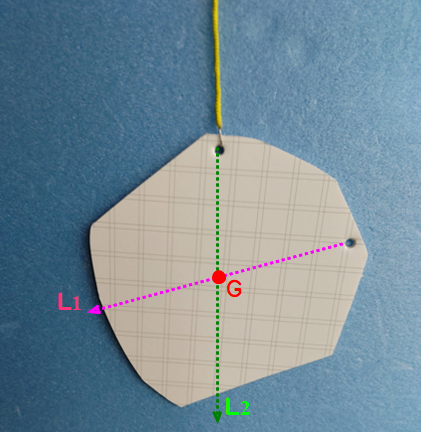
A3 図のように,別の端点からSをひもで吊してその鉛直線をL₂とする.先述したように,重心Gは,①L₁上に存在,②L₂上に存在
⇒ これらを満たすのは,L₁とL₂との交点のみであり,交点が重心となる.
なお,面白い(不思議?)のは,Gを求める際,吊す作業は2回で済む.つまり,3本以上のヒモは不要なことです.理由は「Gは一つしか存在しない」からですね.
見えない重心


■ 上図は,山形県北部にある道の駅で購入したヤジロベエ(竹製トンボ)です.くちばし先端部Pでバランスがとられており,点Pを支点といいます.Pを重心と判断しては早とちりです.
⇒ この場合,重心Gはトンボ体外,Pのやや真下(鉛直線上)付近に存在します.
⇒ 重心Gが支点Pの上(一致も含め)に存在すると,点Pで物体全体をバランスよく支えることはできません.ヤジロベエを逆さにして試してください.
※本blog「竿灯をコントロールできるワケ」を参照ください.

■ では,50円玉を見てください.重心はどこにありますか?
⇒ もちろん中央の穴の中心です.
⇒ あるのでしょうが,見えません.
⇒ その重心で全体を支えることもできません.
何ともいらつかせる重心ですね.
<補足>
■ 「重心が一つしかない」ことの解説ですが,自分としては”オリジナル”と思っています.あまりにも当然すぎて気にしないヒトが多いでしょうが.
■ 背理法や存在定理を扱う際,大上段に構えての指導展開がフツーですが,日常生活の中でごく自然に誘っていくことも重要ですね.重心は格好のテーマです.
■ 次回テーマは「三角関数に罪はない」(予定)です.政治家が議会で,数学,その中でも三角関数を取りあげるケースがままあります.つい先日も.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


A2(1)について、「S1とS2の重さが一致しないなら、L1は動くはず」と言えるのはなぜですか
ほ 様
ご質問ありがとうございます.
鉛直線は,左右の重量バランスがとれた結果の直線になります.野球のバットを横にして指で支えて水平にできたとき,その点をバットの重心というのと同様です.
したがって,「S1とS2が一致しない ⇒ L1は鉛直線にはなり得ない ⇒ L1が微調整で多少動き,静止する ⇒ S1とS2の重さが一致」という主旨の説明でした.時間の流れが逆になっており,分かりにくくなったかも知れません.ご指摘,ありがとうございました.