題意と導入
落語やお笑い漫才は,まず「出だし」,つまり,導入部分でその演技評価がおおよそ決まりますよね.中には,ステージに登場するだけで笑いをとる方もいます.授業と同じですね.
授業の感想2点
(1)昨今の授業で気になるのが,冒頭で「今日のめあては,○○をめざそう」と示すパターンの多さです.確かに,目標を明示して授業に向かう姿勢は大切です.しかし,必ず冒頭で,かつ,結論をダイレクトに子どもたちに示せという意味ではないはず.
授業の進め方も柔軟でなければなりません.極端な話,授業の最後に「実は,今日は○○ということやったんだよ.しっかり身に付いたようでうれしいです」と目標を再確認する授業があってもよいのです.
(2)中高校では,進度のこともあり,ある日の授業が「問題解き」からスタートすることも避けられません.その際の導入は,普段以上の配慮が必要です.題意を踏まえない導入は,「問題のための問題解き」で終始しがちです.例を挙げましょう.
◎巧みな導入 ×稚拙な導入
- 長さ20mのロープがあります.このロープで長方形を作るとき,面積が最大となるときの長方形とそのときの面積を求めなさい.
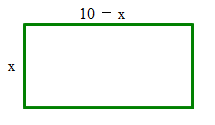
<×導入&展開例>
今日は教科書10ページの例題からですね.まず,題意を読み取ってください.
比較的楽ですよね.まず,縦辺の長さを xmとします.すると横の辺の長さはどう表せますか?
今日は8日だから出席番号8番の△君,どう?
20-x ですか?
よく考えたかな.18番の○さん,どうですか?そう,10-xだよね.
面積をyとすると,y=x(10-x)となります.最大値を求めよということだからxの変域を押さえる必要がありますね.
28番の●君,答えてください.
-----(以下略)-----
×としたい箇所はたくさんあります.
① 教科書ページで指示する導入です.今どき・・・という感じですね.
② 進め方のパターンが「発問→指名」の単一形.また,出席番号順の指名も,今どき・・・です.
③ 誤答した△君へのフォローがない.数学が嫌いになる一因をこの先生は作ったかも知れません.
まだまだありますが,最大の「×」は,
④ この例題(教材)がもつ肝心の意味を深掘りしておらず,教材のよさを活かしていないという点です.
授業の「軸」
<こんな展開はどう?>
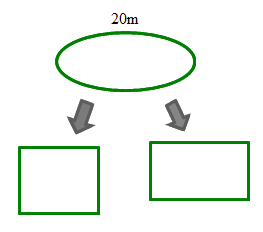
これは,ロープの輪っかで長さは20mです.巨人がいて,この中に左右2本 の指を入れてピンと張ると長方形ができますね.
指を動かすと,長方形もいろいろ変わります.
ロープの周の長さは20mで一定です.ここで何か数学の問題ができませんか?.
面積? なるほど.それでいきましょうか.
暗算でいいかな.縦の長さが3mのとき,面積はいくらになる?はい,21m²で正解だね.じゃ,縦の長さが6mではどうですか?
もっと続けてもいいんだが,これらは算数レベルでみんなには失礼だ.高校数学にしたいのですが,何か提案はないですか?
(中略)
ところで,何か感想とか疑問はないですか?.
A君,何か言いたそうだね.なるほど,面白いこと言うね.みんなに聞こえるようにもう1回言って.
皆さん,聞いた?.周の長さが20mと一定値なのに面積が変わるのか,と思ったそうだ.
← この声を引き出せるかどうかが大きなポイントになります.自発的に出ることがベスト.つまり自由な声が出せるような空気感がふだんから教室内にあるかどうか.
しかし,この構築は至難の業です.
なお,近年,グループ協議を取り入れ意見や声を求める展開が盛んですが,自然さに欠ける場面とも出会います.
協議形式があらかじめプログラムされている出来レース的というような印象?.
A君の疑問は貴重です.大いに活かしましょう.
さきほど計算したように,長方形の形で面積が違いましたね.縦の長さはどこまで小さくなれるかな?0mか.そのときは,長方形とは言えない.線分だね.ムリして面積公式にあてると,その値は?.そう,0となり,これが最小値です.
ということで,「最大値をとるときはどんな長方形か?」という問いができるわけです.
今日の目標(めあて)は「長方形の面積の最大値を求めよう」です.
最大値を予想してください.25m²ですか.あちこちから同じ答えが出てきましたね.つまり正方形のとき最大値となるということですね.当たっているようだけど,キチンと理由を述べていきましょう.

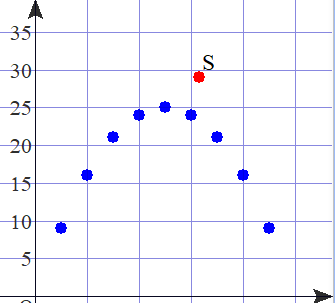
← 多くの場合,生徒は辺の長さを整数値として何例かを比較計算して,直感的に正方形にたどり着きます(格子点にしか目がいかない).
上図でSのような点は本当にないのか?疑問を持たせたいものです.
そこで,改めて文字使用の必要性・よさを確認すること.文字xを用いざるを得ない状況に「追い込む」こと,このプロセス(※)は大切です.
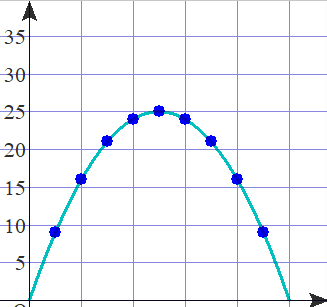
周の長さが一定値でも囲む面積は変わる!このハット感が次に活きます.
解法マニュアルに沿って,縦(or横)の長さをxとして計算を始め,正解にたどり着く生徒の中にも,実はこの認識がないママ進めていることもあります.
⇒ 計算はできたとしても思考力や知的好奇心は高まっていない
学習の進んでいる生徒たちには,定理「関数 f(x) が閉区間で連続ならば,f(x) はその閉区間で最大値・最小値をとる」を紹介することも意義があります(← 存在定理の一例として).
また,囲む図形を四角形から五角形,六角形と増やしていくことで,最大面積となる形を推測させることも可能となります.(← 周の長さ一定の閉曲線で囲まれた部分が最大面積を持つとき,その形は何か?)
上記の授業を見る限り,上記「稚拙」先生は,授業展開面も稚拙であるだけでなく,教材自体を「流れの中」で位置づけていませんね.
つまり,終始,問題のための問題という単発扱いをしています.残念!
■ にほんブログ村のバナーをClickしていただければ幸いです(最初:左, 次:
右).