3< 円周率 <3.5 を確認する
定理や法則はすべて証明した上で次の段階へ進みたいものです.しかし実際は,π(円周率)=3.14159・・・のように,定理・法則の「ユーザー」と割り切るしかない例も少なからずあります.ただ,その「割り切り方」は大切ですね.

「詳しくは大学で習うが,ここではおおよその値でいこう」はまずまずとして
(※実際は大学でも関心をもつヒト以外はムリ)
「ワケはいいから結果は覚えておけ」はワーストかと.
円周率って何だっけ
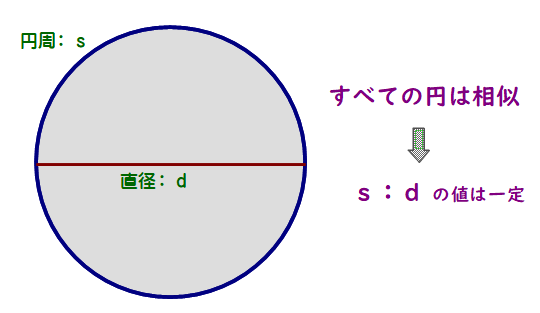
■ 円周率とは,円の 周(s)と直径(d)との比
つまり,s:d (=s/d)をいいます.
point は次の2点.
① すべての円は相似より,比
$$\frac{s}{d}$$は一定値となる.
② 古代から円周率は3程度であることは知られていたが,後に無理数であることが証明された(循環しない無限小数)ので,(仕方なく)文字定数:πが当てられた(⇒ πはギリシャ語で”周”の意味).
特に,直径d=1 のとき,s/d=s より
π=円周(の長さ) である.
3<π : 楽勝!
■ かつて,東大入試で「3.05<π 」の証明が出題され,受験生や関係者を面食らわせました(’03).今でも良問と思っていますが,採点はさぞタイヘンだったでしょうね.
■ ここでは,まず,3<π を示します.
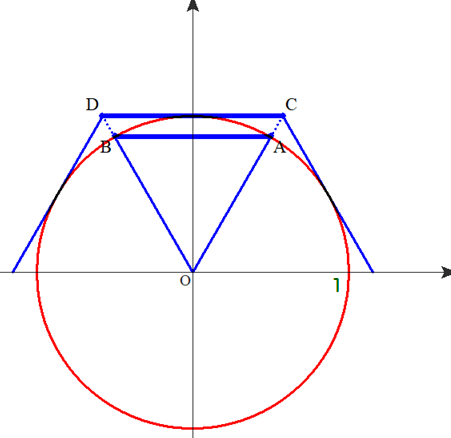
■ 上図は,半径1の円に内接・外接する正6角形を示しており,△OAB, △OCDは正三角形です.
すると
AB=1(AB=半径OAより)
AB<弧AB(AからBへの最短距離=AB)
これらを6倍すると,6 < (半径1の)円周
よって,直径1 とすると,3 < 円周率π が示されました.
次に,π < 3.05 を示します.
π< 3.05 は?
■ 上図で,外接する正6角形に注目して,π< 6×CD を示しましょう.
CD=2/√3 (※)であり, あとは弧AB<CD から論が展開できそうですが,コトはそんなに簡単ではありません.
※△OCDの高さ:1 → 高さ:1の正三角形の1辺は三平方の定理より2/√3
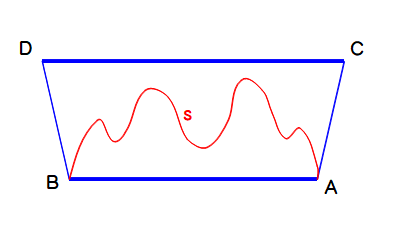
■ 図で,曲線sは,線分ABとCDに挟まれておりますが,AB<s は正しい.しかし,s<CD は必ずしも成り立ちません.
このように,下限は最短コースを根拠にして示されますが,上限はカンタンではありません.東大の問題も下限の証明でしたね.
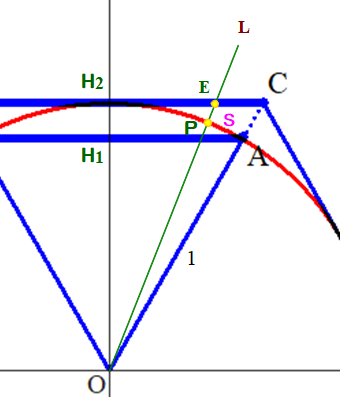
■ 上図で,Pは弧AH₂上の動点,直線OPをL, CH₂とLとの交点をE, ∠POH₂=θ とします.
θを横軸,yを縦軸にして,θを0≦θ≦30° の範囲で動かしたとき,y=線分OE をグラフにするとおおよそ下図のようになります.⇒ 弧AH₂を線分に変換する操作に相当しています
ここで,OP=1(半径) で一定であることより,y=OE=PE+1
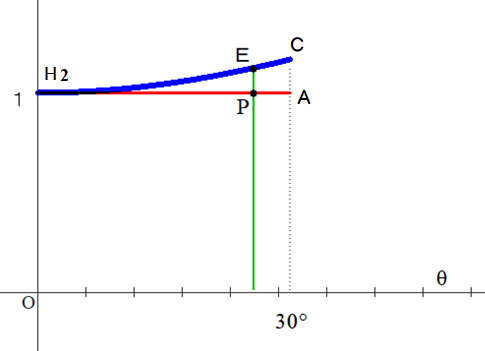
■ 図から,AH₂間の最短コースを考えると,s<弧CH₂ であることが分かります.
また,上述したように,CD=2/√3 なので,外接正6角形の周の長さは,12/√3=4√3 です.
よって,円周(半径:1)の長さは4√3 より小さいことになります.
直径1の円にすると,円周:2√3≓3.46
したがって,π<3.5 が示されました.
⇒ 線分PEの長さをθの関数と見たとき,増加関数であればよいわけです.
循環論に注意
■ かなり苦労して,π<3.5 を示しましたが,そんなメンドーなことをしなくても
△OAH₂<扇形OAH₂<△OCH₂
からラクに弧AH₂<CH₂ が導かれるとの見解もありですね.
しかし,この論法は,扇形OAH₂の面積公式:1/2r²θを用いており,半径rの円周:2πr という結果を利用していますので,これから証明しようとしている円周率πを先取りしていることになります.
これを循環論法と言い,陥りやすいエラーです.
■ アルキメデス(ギリシア)は,円に内・外接する正96角形を用いて,π≓3.14を示しました.
約2300年過ぎて,今回,正6角形を用いて,はるかに精度の緩い円周率を得ました.足下にも及ばないとはこのことですね.
<補足>
■ π<3.5 について,弧度法を使って説明すると「循環論法」になります.そこで,弧度法を知らないという前提で回転角30°を「均等分割」し,横軸の変数にして,回転角量を直線上の点に変換しました.
■ 次回テーマは「球の体積公式」(予定)です.この公式も「天下り式」定理の典型ですね.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).