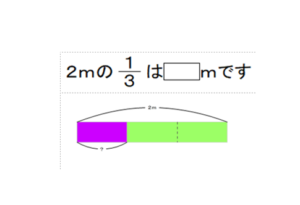
y’:意味わかんないが計算はできる
■ かつてある学生(工学系2年)が述べた言葉が残っています.「クラスのAが言うには,『微分も積分も毎日,計算しているんだけど,ホントは意味がわかっていないんだ』と.この先もっと大変になりそう.彼の場合,どこから手を付けたらいいのでしょうか」.微積分に限った話ではありませんが,思い当たるところ多々あります.
■ 一方,「今はわからなくても,計算を続けるうちにいつかわかるよ」という指導者の助言も耳にします.

■ 今回は,この意味理解なしの計算をとりあげ,ややもすれば機械的な計算で終始しやすい微分に焦点を当てましょう.
グラフをイメージしよう
Q1 下図で,直線gは,y=f(x)の導関数y’ を表しています.y=f(x) のグラフをイメージしてみてください.
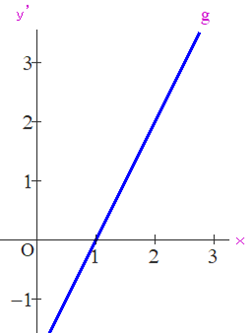
■ 数学に関心ある方の中には,「何でコレが問題になるの?」と感じる方もいることでしょう.しかし,コトはそんなに甘くありません.私見ですが,高校生一般(勤務校に限定しない)の正解率は,1/3以下ではないか(もっと低いかも)と推測します.
■ そして幸か不幸か,微分計算の結果は,結構よいのです.なぜなら,微積計算の大半は,ルールに従えば「分数計算の復習」という側面がかなり強いからです.
■ こうした状況は「数学ではよくあることだ」と達観せず,何とか改善を図っていきたいもの.「数学の学び」が結局,「点数をとる・とらせる」ということに帰着してしまう風潮はよろしくないですよ.
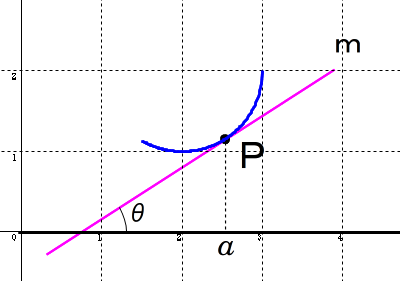
■ 微分係数 f'(a) は,定義により曲線 y=f(x) 上の x=a に対応する点Pにおける接線の傾きを表すのでした.つまり,上図で,f'(a)=tanθ というわけです.← ちなみに接線の英訳は,tangent
■ したがって,たとえば,f'(a)=1 ならば,θ=45° となり,f'(a)=-1 ならば,θ=-45° です.
■ くり返しますが,y’の値=接線の傾き です.”意味理解なし計算“派の高校生・大学生は,この「基本の基」が 徹底されていません.「それは説明した」と言う担当者もいますが,イメージ化のツメが甘かったという印象を受けます.
■ 改善策を一つ提案します.それは,計算だけでは対応できないテスト問題を作成することです.方法としては邪道でしょうが,学習者へのメッセージになり得ると考えます.かつて,東大入試に三角関数の加法定理の証明がストレートに出題され,結構な話題になりました.実際,予備校や高校(一部)の講義内容にも影響を与えたようです.
■ 冒頭の問に戻ります.
<図1>
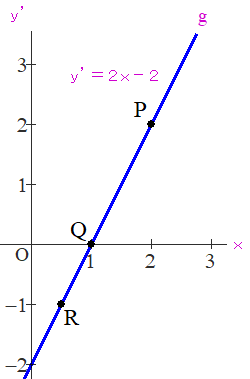
Q1’ 上図で,直線gは,導関数y’=2x-2 を表しています.では,元の y=f(x) のグラフイメージ(おおよそ)を示してください.
A1 代表点P,Q,Rの3点で考えてみましょう.各点のy’の値は,それぞれ 2, 0, -1 です.それらの値は,接線の傾きを表しますので,接線の様子は次の図2のようになります.※y=f(x)が通る点が不明(積分定数が任意)なので,第1象限の適当なところにかいています.
<図2>
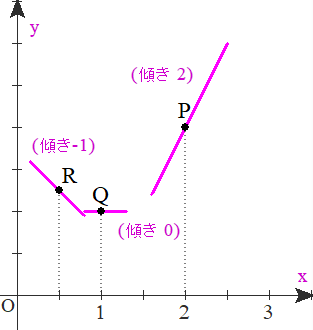
■ 図1と図2を比較して,この両者関連の「ナットク感」はいかがでしょうか?
①図1で,点の縦(y’)座標の値=接線の傾き です.例:点Rのy’=-1,よって, θ=-45°
②図1のように,点QはRより下になり,点PはRより上になる
③図1で,点Qの下部分(x<1)では,y'<0 よって,y:減少↓,Qの上部分(1<x)では,y’>0 よって,y:増加↑
④図2において,PQRの3点以外に,点を無数に増やしていくと,下図のような曲線(青の放物線)が見えてくる.
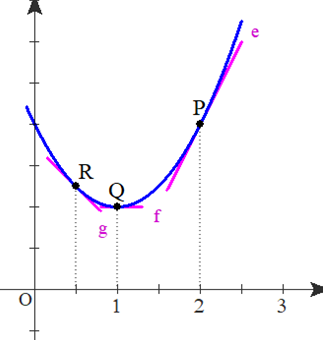
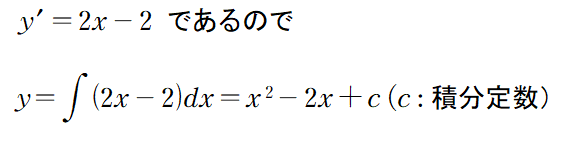
■ 計算式では,積分すると上記のように2次関数が求められるので,説得的です.しかし,イメージとして,すなわち,「図形的に理解する」ことはどうでしょう.
Q2 次の図1で,導関数y’=f'(x) のグラフが示されています.このとき,図2の①~⑥から,元の y=f(x) のグラフを選んでください.それを選んだ理由も述べ,さらに,図1の点Pについてわかることを解説をしてください.
<図1> <図2>
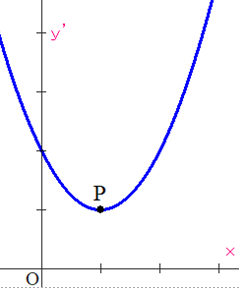
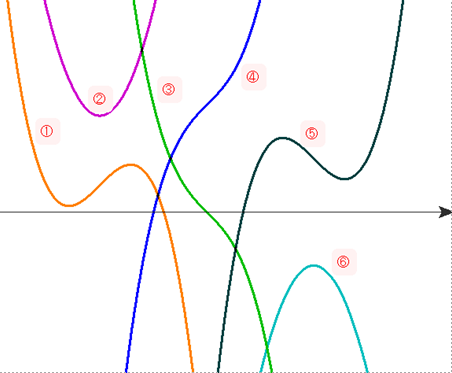
A2 正解・・・④
理由・・・図1より y’ はX軸よりつねに上にある.つまり,一定符号で y’>0 → yは単調増加関数.したがって,④のみが該当.
点P・・・単調増加であるが,Pを境にその増加の仕方が変化している.→ Pの左側:y’の値が減少しているので,接線の傾きは右上がりであるものの次第に緩やかになっている(上に凸).Pの右側はそれと反対(下に凸).点Pを変曲点という.
■ Q2の例で示したように,変曲点はy’の変化の様子,つまり,y’の変化率=y”(第2次導関数)を求めればよいことになります.
■ 関数の変化は微分法で把握できます.接線の傾き具合(y’の値)で,まずは局所的に判断していくというのが微分の考え方の出発点です.接線=一次関数ですね.一次関数を軽く見てはいけません.一次関数は”比例”の延長線上にありますので,比例の思考が小中高の理数を貫いています.
<追記>
■ 次回テーマは,「数学用語アレルギー(第2弾)!」です(予定).算数・数学の独特用語でヒトビトに「警戒心」や「拒否感」を与えているとすれば,それは解説する側にまず第一義的な責任がありましょう・・・.
■ 本ブログの冒頭とエンドの2個所に,「にほんブログ村」のバナーがありますが,それぞれClickしていただければ幸いです.