分数:やっぱり難しい
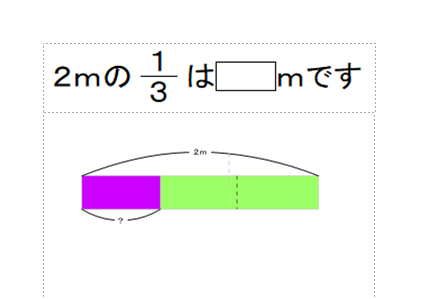
Q 長さ2mの棒の 1/3 はいくつですか? A 2/3mです.
■ 何気ない質問・答えですが,小学生(2,3年生あたり)がよく答えられるな~と思います.嫌みではありません.心底,そう思います.やっぱり分数は難しいです.
■ 上のQについて
① 1/3 m と答える子どもが必ずいます.大人も同様.
② 1/3 , 2/3 と二つの分数が登場しますが,それぞれの意味・役割が違います.
③ 1/3 や2/3という表し方に,そもそもの抵抗感ありませんか(これらも数なのかと).
エッ!同じ分数でもイミが違う


■ ” 長さ2mの棒の1/3 “
この1/3は,”棒を3等分した1つ分”を表します.分割分数といい,一般的には「等しく分けたウチの□分」という解釈になります.「分割する」という操作が根底にある訳です.
■ ” 2/3m “
この2/3は,長さ,つまり,2/3(=0.666・・・)mという量を表しているので量分数といいます.
■ 端的には,量分数はmやkgなどの単位付き,分割分数は単位なし・数字のみということになります.
<参考>「分割分数から量分数への指導に関する一考察」(’16 三重大・中西,兵庫教育大・西村)
分数・・・2数から新たに数を作り上げたモノ
■ 次は,代数学(学部1年次あたり)の一部抜き書きです.

■ 上記説明文に対して,学生は・・・①スイスイ理解できる ②全く受け付けない の2タイプに大別できそうです(中間はいないかも).2極化現象という言葉が当てはまりますね.
■ ②の方へ → 整数(・・・-2,-1,0,1,2,3・・・)だけの世界から,有理数(分数)まで拡張構築していく際の,最初の約束事を示しているのが上記説明文です.
(a,b)が a/b に相当します.すると,(a,b)+(c,d)=(ad+bc,bd) は 通分のルールを主張しているわけです.この視点に立つと説明文全体の理解がスムーズになりますね.
■ 2整数aとbで,数(a,b)をつくる,具体には,例えば,2と3で,2/3 という新たな数(分数)をつくり上げたということです(整数環から有理数体への拡張).
子どもの心情(抵抗感)に思いを寄せたい
■ 既存の数から新たな数を構築する・・・かなり高度な思考が求められます.
0と1で,9より1大きい10という整数をつくる(10と「書く」←10進法のルール).
2と3で,2/3という数をつくる.分数と名付け,主に「分割」と「量」の2側面をもつ.
3から√3という数をつくる.無理数と名付け,イミと計算ルールは・・・.
1と 虚数単位i で a+bi という数をつくる.複素数と名付け,計算ルールは・・・.
■ 上記解説文で有理数体の導入を示しましたが,かなりの抵抗感を持った方がいると推察します.
子どもは,新しい数や概念が紹介されたとき,同じような心情に陥る(抵抗感を抱く)ことも多々あります.
具体的な改善策の提示はできませんが,まずは,心情理解が肝要かと.その後に指導方法を練りましょう.
<追記>
■ 次回テーマは,「導関数y’は大丈夫?」です(予定).微分計算自体はラクといえば楽なんですが,さて・・・.
■ 「にほんブログ村」のバナーがありますが,Clickしていただければ幸いです(最初は左,次に右).