“あれ”が苦手（あれ：直線のベクトル方程式）

ベクトル方程式から直線や平面をイメージするのはケッコウ辛いことです．ただし「直線 ⇔ 一次式y=ax+b」のナットクもそんなにラクではありませんが．

ベクトルは向きと大きさのみで決まる！

■ ベクトルは｛向き，大きさ｝のみで決定します．

つまり，位置はどこでもよい ⇒ 平行移動が可能

たとえば，北向きで大きさ2のベクトルは，始点が東京でもパリでもベクトルとしては同値になります．

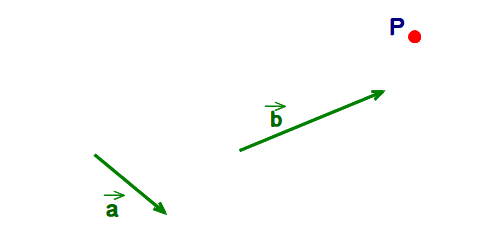
■ 上の主張の意味 ↓

ベクトル方程式で直線をイメージする

■ 以上のことをまとめて主題の直線に近づきましょう ↓

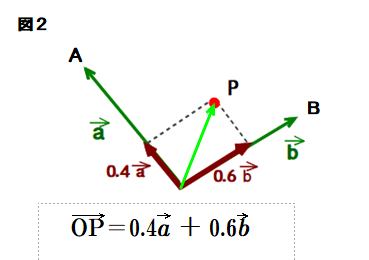
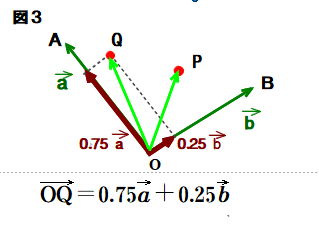
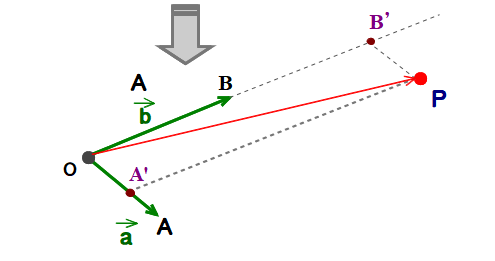
■ 点A,Q,P,B の並びに注目してください．

点P,Q が直線AB上にあることが予想できますね．

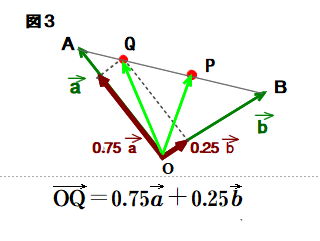
■ どうやら各ベクトルの係数にヒントがありそうです ← 0.6と0.4，0.75と0.25

直線のベクトル方程式に親しもう

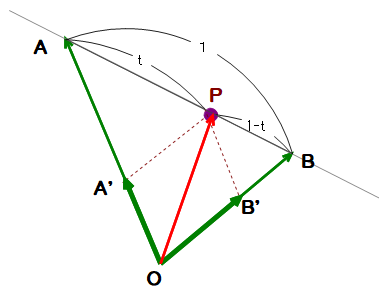
■ 直線のベクトル方程式は，通常，AP:PB=m:n として内分点公式や△OAPに着目してベクトルの和から導きますが，ここでは中学校で学んだ相似形の性質をフルに活用してみます．

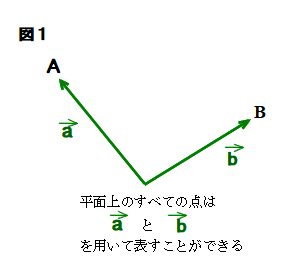
上図で，点Ｐは直線AB上にあり

AO∥PB’ ，BO∥PA’，線分AB=1, AP : PB= t : (1-t)  とします（一応，0<t<1 としておく）．

△AA’P∽△AOB より，OA : OA’=1 : (1-t),   OB : OB’=1 : t となることから

　　　OA’=(1-t)OA,  OB’=tOB ･･･①　が成り立ちます．  

＜補足＞

■ 次回のテーマは「学習の進んだ子ども(5)」（予定）です．

■ にほんブログ村ランキング（数学教育）にかかわってバナー↓のclickをお願いします（宣伝が多く恐縮です）．

■ もう一つ．「ブログみる」の紹介ブログ村制作のblogを見るためのアプリです．世は正に情報過多の時代．しかし1日は24時間しかありません．できるだけ良質のブログと出会いたいものです．ブログ村が総力を傾注して立ち上げた

ブログみる

に関わっていきましょう．