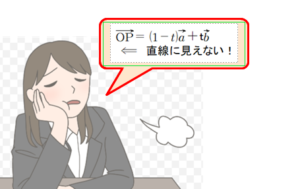
「変化 ⇒ 即,比例」 という思い込み
比例は極めて重要な変数間の関係です.テストでは小中高を通し頻出され,また,自由研究の作品でも,計算自体は比例という例が少なからずあります.

比例は重要 ⇒ だからこそ比例しない例をしっかり!
■ 任意の曲線も,微視的に観察すれば,線分の集まり ⇒ 直線的変化 つまり,比例ですね.これが微積分へと発展します.
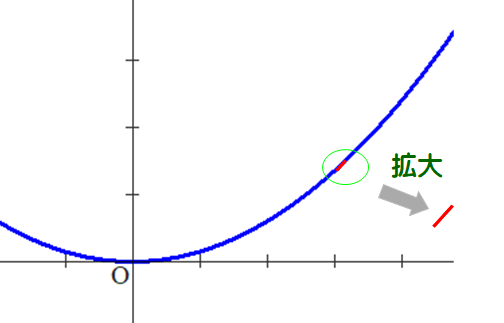
■ このように,比例は変化の大御所であることは間違いありません.
そうであればなおさら比例しないケースをしっかりと押さえておくことが変化全体の理解へと進みます.
■ A大学数学教育研究室では13年前より「なるほど算数・数学」なるプロジェクトを立ち上げ,近隣の小中高で「学生出前授業」を実施しています.
ある高校での様子を紹介します(多少脚色).

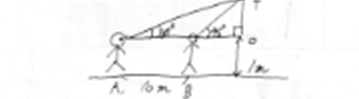
■ 解説は省略します.本問設定の背景には,日常生活に数理の視点を当てる意味合いがありました(担当学生S1さん談).
⇒ 大学共通テストでも 試行テスト,’22本テスト, ’24本テストと測量に係わる出題がされました.
■ (2)の問について,高校生A1さんと担当学生S2さんとやりとりが印象に残っています.
S2 「高さが2倍になるので角度も2倍としたワケだ」
A1 「はい.ダメですか?」
S2 「45°×2 で90°か.でも仰角が90°のとき,見上げる顔はどうなる?」
A1 「あれっ?真上になる・・・??」
S2 「今わかったことを整理してみよう.すごく大事なことなんだ」
(以下略)
⇒ この例は,関数y=tanx が比例関数でないことを示しています.
⇒ x(入力)が2倍になれば,y(出力)も2倍になる! は成り立たない
復習の在り方
■ 上記の y=tan2θ についてS2さんの解説は,復習の在り方について意義あるヒントを提供しています.

■ 通常,復習と言えば,以前習ったことをそのママ・その順で再度学ぶというケースがほとんどです.
⇒ 学習者の立場からは既視感のあるいつか見た景色であり,新鮮味も欠け,学びの効果はあまり期待できないと思います(たぶん).
次のような攻める復習の展開例はどうでしょう.
■ T:数学リーダー,Ai:生徒(三角比,三角関数を履修済とする.i=1~4)
T:先程のA1さんの発言は,高さが2倍になれば仰角も2倍になるだろうという見通しだったけど正しくなかったね.何しろ仰角が90°のときは,天井が無限に高くなるので.でも,A1さんの答は実に意味ある「歓迎すべき」間違いなんですよ.
変数がk倍になれば, 結果もk倍になる,という関係を何て言いますか?
A2:比例かな
T :ハイ,そうですね.勉強時間と点数はどう?つまり,勉強時間を2倍にすれば,点数も2倍になりますか?
A3:なるときもあるが,そうならないことが多いと思う.
T : さっきの「歓迎すべき間違い」より,y=tanx という三角関数は比例関数ではないことがわかったワケです.
式で表すと,tan2θ は 2tanθ とはならないのです.
では y=sinx はどうですか? sin2θ=2sinθ が成り立つかどうか.
A4 :どう考えるんだ?さっきみたいに図もないし.
T :皆さん!初めて見るように式を捉えているけど,sin2θ や tan2θ とホントに初対面ですか?どっかで会っていない?
A1:アッ!2倍角公式だ!
T :そうだよ.あの憎らしき三角公式群の代表だったね.
sin2θ=? tan2θ=? それぞれどうでした?
A1:sin2θ=2sinθcosθ で,確かに比例関係ではないです.
T :cosθが付いちゃうからね.
(以下略)
<参考> \[ cos2θ=cos²θ-sin²θ, tan2θ=\frac{2tanθ}{1-tan²θ} \]⇒ 以上の展開は,「関数の比例」という視点から既習のsin2θ,cos2θ,tan2θ (2倍角)公式の見直し・再確認を図ったと言えます.
なお,θ>0でθ≓0 のときは,cosθ≓1 より,y=sin2θ=2sinθcosθ≓2sinθ となり,ほぼほぼ比例関数.また,θ≓45°(π/4)のときは,tan2θの分母=1-tan²θ≓0 より,tan2θ→+∞ となります.
<攻める復習のイメージ>
習った事項について
Ⅰ 別の視点から見直し,再認識する
Ⅱ これから習うことに関連付け,予習にも踏み込む
⇒ 復習の一つの形に「補習」と称する半ば強制的な学習もあります.中には不本意ながら出席する子どもも多いことでしょう.
その際,「攻める復習」は効果あります.子どもに「補習に参加した方がトクだよ」と思わせたらサイコーですね.
<補足>
■ 次回テーマは「ベクトルの和」(予定)です.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.