暗記と数学
■ 公式や定理,筆算の方法など,数学を学ぶ上でも(他教科ほどではないが)”暗記”と付き合わねばなりません.どう対応していますか?

数学リーダーの「対暗記」スタイルは次の3タイプに大別されます(私的観察).
数学リーダー3タイプ

①論(ワケ)は棚上げ.とにかく正解させるべくレッスンを重ねる.巧みな語呂合わせなど工夫する
②論と計算レッスンを平行して展開して自然と公式を身に付けさせるよう努める
③姿勢に一貫性がなく,あるときは①,別の場面では②.迷い人?
■ この中で①②両者の違い・溝は深くて埋まりそうもありません.
②→①へのチェンジは簡単ですが,①→②へは困難です.
なぜなら①タイプのリーダーには”学び=テストで点を取る“という価値観が根底にあるからです.
以下,①:暗記リーダー,②:理解リーダー とします.
合った! vs わかった!
■ 「問の答えが合った!」と「考え方がわかった!」・・・どちらも子どもは喜びますね.
数学リーダーへ:どちらの「子ども像」を選びますか?
両方という方へ:どちらに重きを置きますか?
例を挙げて考えましょう.
九九
小2でかけ算を習います.少なからずの保護者と暗記リーダーは九九の暗記徹底に躍起になります.
「7と8の段が弱いね!」「フロに入って9×9 までやってみようか」
■ ある理解リーダーによる授業の様子です.
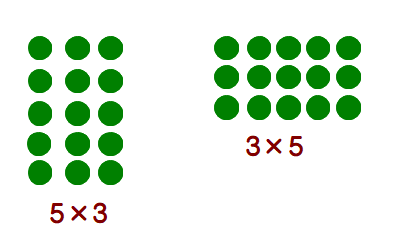
■ 「5・3 は?」「ゴ・サン15で~す」「左の絵といっしょに覚えましょう」
「右の絵は何を言っていますか?」「3・5(サン・ゴ)で15で~す」
「あれ?答えが同じ15.どうして同じになったの?」
「絵の置き方を変えただけだから」
(以下略)
■ そして,理解リーダーは3年への進級が近いころ,詰めの追い打ちをかけます.それも唐突に.
「5+7+5+7+7+7+5+5+7+5+7 はいくらになりますか?」
と板書しました.「エーッ!長~い」という声.
何人かの小2生は順に足し算を始めています.
その後,理解リーダーは,上式=5×5+7×6 となることを引き出し
①かけ算が「同じ数の足し算処理の合理化」のために誕生したことの再確認
②お経みたいな5・5(ゴゴニジュウゴ),7・6(シチロクシジュウニ)が活躍する場面に立ち会わせ,かけ算のよさを感じとる
ことをねらいとしてあの手この手と創意工夫を重ねているわけです.
マル暗記の悲哀
■ 暗記リーダーの多くは主張します.「この公式を覚えなければ先へ進まないのだ」「テストで0点だけは取らせたくない」等々.
自身の創意工夫の代わりに「恫喝(どうかつ)数学」を振り回していませんか?

■ 結局,数学の学び=点を取らせる という「哲学」の反映でしょう.
■ ある高校生たちに
1.732×1.732
のおよその値はどれくらいになる?
とたずねたところ,少なからずの生徒が図のように筆算をし始めました.
⇒ √3≓1.732(ヒトナミニ)と口酸っぱく暗記させられても,√3の意味理解が伴っていない場合の滑稽(悲しいくらい)な事例です.
■ マル暗記指導の極めが「三角比・三角関数値表棒暗記」指導です.
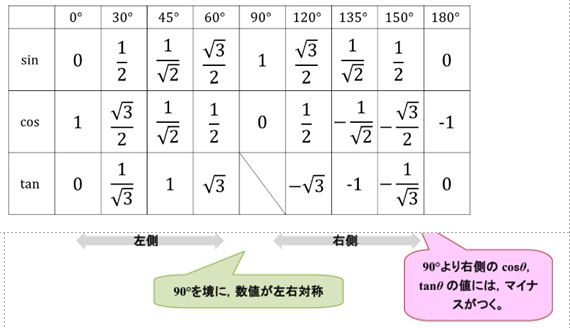
■ 暗記指導「被害」に合った高校生や大学生(理工系含む)を見るにつけ,これなら「三角関数を教えてもらわなかった方がよかった」とさえ思います.
⇒ 頭の中は「有名角だらけ」ですので,三角関数の連続性自体の理解もあやしい限りです.
⇒ 百歩譲って,sin110°の値と√3/2 との大小ぐらいは押さえてほしいもの
■ (昨今の実態に業を煮やしたと思われる)文科省は,大学共通テストで生活数理(測量的な場面)を取り入れた出題をしています(試行, ’22, ’24本試).有名角中心の指導をしてきた学校への警告メッセージでしょう.
暗記指導への対案
■ 暗記リーダーが「テストの点」にこだわっているとすれば,「テストの点」においても理解リーダーによる指導結果が上まわることを実証することがカイゼンへの近道です.最後に子どもたちが判定してくれるでしょう.

<対応の具体例>
■ 九九
前述したように,個数(量)を〇の数で表すなど,イメージ図(絵)を用いての学びは次に活きます.
古文や漢文と異なり数学においては単なる棒暗記はお経と同じ(お寺さん,すみません)
⇒ 「今わからなくても覚えなさい.いつかわかるときがくる」は方便であり実証されておりません.
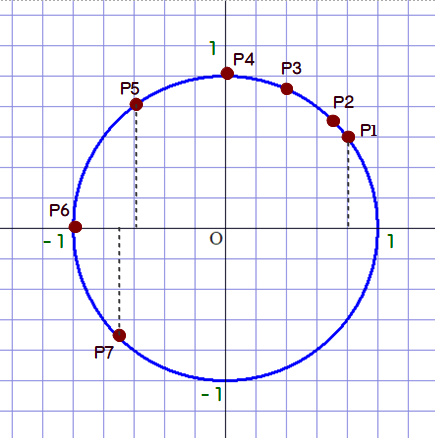
■ 三角比・三角関数
①単位円周上の動点Pが1周するとし,第3,4象限も含めた方がベター
⇒ 三角比で第1,2象限に制限される理由は学習指導要領への対応のため.数学的にはメイワクな話
②任意の動点のおおよその座標を読み取る
⇒ 予想以上に読み取れません!やってみてください.点を打つことはあっても読み取るレッスンは受けていないようです.
⇒ 値は概数でよいとしますが,P2,P4,P7など「有名角」に係わるときは,正確な値を求めさせる.
例 P1(約0.8, 約0.6), P7(-1/√2, -1/√2)
③θ:各動径とx軸とのなす角 として
θ ⇔ 各点の座標値 として,関数記号としてsin, cos, tan を導入する (以下略)
※例 cos120° ⇒ ①単位円の図をイメージさせて答えを求める(イメージできないときはノートに図示させる).②cos125°との大小を確認する
最初は時間かかりますが,理解度・定着度は格段に違います.
※「cos125°との大小比較」等を定期テストに出題すると効果はてきめんです(この種の意外出題は全国学テで国も実施しています).
<補足>
■ 「1789年フランス革命」と「sin120°=√3/2」が暗記同列扱いは断じて許されないと考えてきました(世界史には恨みはありませんが).
■ 次回テーマは「数学秀逸たとえ話」(予定)です.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.


