導入時つまずき⇒ リカバリー:ほぼ無理
数学の進め方はサマザマですが,やはり違い(≓差)はあります.特に導入部分で顕著に表れます.その際,”めあて”に要注意!
芸人から学ぶ

■ 教壇と舞台ステージには共通点が多々あります
⇒ どちらも演者の語る,①中身 と ②語り方 がpoint
⇒ 特に,出だし(導入部分)でつまずくとリカバリーはまずムリ
※当方,長年にわたり数多く失敗してきました
■ ステージに登場するだけで笑いを取る芸人がたまにいます.導入部分の苦労が不要と言うより,それまで蓄積された「芸財産」が導入の代替になっていると解釈すべきです.
導入⇒”安直めあて”とすり替え
■ 本人は無意識かも知れませんが”安直”なめあてを導入部分にすり替えてしまうことも散見します.2例紹介します(導入例A, B).
Ⅰ 指数(中1数学)・・・次は教科書の説明文です.
いくつかの同じ数の積を,次のように表すこともあります
5×5×5=5³ ・・・右上の小さい数3を指数といいます

A 「では授業を始めます.今日のめあては『同じ数を何回もかけるときの表し方を学ぼう』です.まず・・・」
(以下略)
■ この後の展開はだいたい見当ができ,定義確認→例題→問題演習の流れかと.
Aは「導入=めあて明示」と解釈している例です
⇒ 仮に「協働的な学び合い」としてグループごとに協議したところで 先生による,先生のためのめあて である限り学習効果は期待薄
■ “めあて”の原則は, ①子どもから言葉を引き出しながら作る,②子どもの自分事にする ことです.
これはかなりしんどい作業となります.だからこそ導入時の創意工夫には”熱“が必要なのです.
B 教卓にA4用紙を置いて,以下のような作業を始めます・・・
「ちょっと見ていてください.
①教卓の上でA4用紙を半分に折る ②続けて①を半分に折る ③続けて②を半分に折る ④・・・
様子はわかりましたか.折紙と同じ作業ですね」

「2回折った②を広げると,折れ線でA4用紙はいくつの長方形に分けられるかな?」
「4つです」・・・(b)
「3回折った③を広げると?」
「8つになる」・・・(c)
「最初に戻るけど, ①を広げると?」
「2つです」・・・(a)
「③から進むよ.4回折った③を広げると?」
「16の長方形ができる」・・・(d)

「ここまでの結果をまとめてみると
(a) 2, (b) 4, (c) 8, (d)16 となるね.
何か気の付いたことはない?」
「a→b→c→d と2倍ずつ増えている」
「そうだね.この調子で行くと,5回折ると?」
「(e)32です」
「では,(a)~(e) までを整理した(美しい)式で書いてみよう」
「aはパスして,b:2×2=4 ですね.するとcは?」
「c: 4×2=8 です」
「bの結果を使って”通し”にすると?」
「c: 4×2=2×2×2=8 です」
「美しいね!」
「では,eを美しく書いて」
「e: 2×2×2×2×2 です」
「用紙を10回折るとどうなるかな」
「書けるけど,長すぎて大変.計算も大変」
「ハイハイ.そこで,今日のめあては『同じ数を何回もかけるときの表し方を学ぼう』です.慣れれば便利で計算も速くできるぞ」
(以下略)
※実際に折作業をさせると,2⁶ あたりから折ることがきつくなり,2⁷ からはムリ.「何回まで折れそうですか?」という問いかけも意義深いです.したがって,有名結果 2^10=1024 などへの”親しみ&敬意”も醸し出されるかも
⇒ 量概念の形成にも貢献.「2の10乗は1024」などと気安く言うべからず!ですね.
Ⅱ 無限等比級数の和(高数学Ⅲ)・・・次は教科書の説明文です.

<導入例AとB>
A 前時:無限等比級数の定義,公式の証明を終了
「前回は,無限等比級数の公式を証明しました.今日のめあては『無限等比級数公式を使いこなそう』です.では・・・」
(以下略)
■ この後の展開は
例題解説→演習問題(各班から代表が板書)→ まとめ
の流れでしょう.
⇒ めあて明示が,硬直化・形式化・ワンパターン化 しており,率直に言ってインパクトなし!
B 前時:無限級数 a₁+a₂+a₃+・・・ の和(=第n部分和の極限)について解説
「突然ですが,本校生徒全員に現金プレゼントをします(口約束).ただし,全員に通し番号付けをして1年1組1番から順に,10000円,5000円,2500円・・・という配り方で,一律平等ではないとするよ.では,私はいくらの現金を用意したらよいかな?」

「100万円くらい.足りないか」
「全校生徒は何人いるんだ?500名くらいか.すると,500万円まではいかないので,250万円くらい」
・・・・・
「いろいろな声が出ましたね.ところで,配り方は,前のヒトの半額をもらう,というルールだったね.すると,2500円の続きはどうなるの?」
「1250円,625円,312.5円・・・」

「ハイ,これらの金額を合わせまとめるとどうなるか?という問いかけでした.毎回,生徒に配る額は減るけど総額は増えていくという状況ですね.”ちりも積もれば山となる”となるかどうか」
「前回,s=10000+5000+2500・・・ のような形の式を級数といい,その和も説明しました」
「そこで,今日のめあては次です」
「すべての項が正である無限級数は『ちりも積もれば山となる』ので発散する」は正しい主張か判断しよう
(中略)
「例にした”現金バラマキ”事例ですが,結論を言うと,20000円用意すればよいのです」
「でも生徒数が増えれば総額も増えますが?」
「いい疑問だ.今の意見,聞きました?もう1回言って」
(以下略)
■ 「無限級数 a₁+a₂+a₃+・・・ 」の「・・・」部分の処理が大変ヤッカイなのです.情緒的に理解してはいけません.
通常の和(加法)は当然有限個の数を対象にします.「・・・」が付く場合の「和」をどう合理的に定義・約束をするか.ここが,微積分の最初の関門になります.
⇒ こういった所を押さえないと「計算は出来るが意味は分からない」学生の量産に直結!
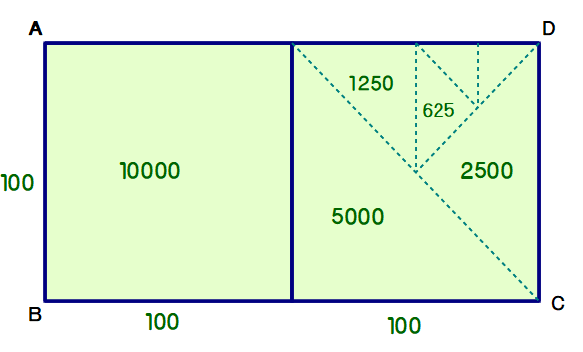
■ 図は「ちりが積もっても山とならない」本問のケースを表しています.
⇒ 長方形ABCDの面積(=20000円)が求める解
⇒ 生徒数は何人であっても総額20000円を超えないことが直感的にワカル
<補足>
■ 指数と折紙との関係,無限等比級数の和を「図形的に表す」ことは,数学を展開していく上で有効な手段です.
■ 次回テーマは「濃度正答率21.6%(全国学テ)はホントか?」(予定)です.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.