近似値は脇役か?
日常生活で距離や面積,重さなど連続量を扱う際,数値は近似値で処理します.しかし,授業・テストとなるとどうでしょう.近似値は”冷遇”されていませんか?
■ 授業やテストでは,近似値&近似式が”主役”になることはめったになく,付け足し程度で解説がなされることが多いようです(特にテストで顕著).
■ なぜでしょうか?
(1)近似値には「2.3ぐらい」「約55%」などのように,答にある種の幅が出来,「数学は答が一つだ!」という原理原則から外れ,子どもたちからは歓迎されていませんね.
(2) テストでは,”採点がメンドー“ということも否定できない事実です.特に,公共性高い入試では敬遠されがちでしょう.採点基準が難しい!から.
■ 突然ですが,身近な利子の話題です.
銀行利子の虚しさ
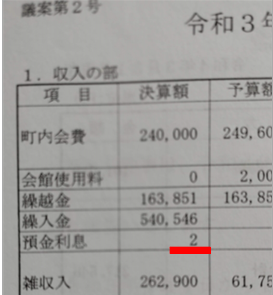
■ 上の表は,所属する町内会会計の一部です.会員数50軒程度の小さな規模で,年間総予算100万円程度で運営しておりますが,1年間の銀行利子2円という額を再認識いたしました.まぁ「ただ同然」ですね.
■ 世界でもレアケースとも言うべき極低金利から,ある近似式が思い起こされます.
複利計算 vs 単利計算
■ ここでおさらい.100万円を年利率15%で借り入れるとします.
単利:1年後の返済額は115万円,2年後は130万円・・・x年後は,元利合計: y =15x+100 ⇒ 1次関数
複利:1年後の返済額は115万円,2年後は115万×1.15=132万円・・・x年後は,y=100×1.15^x ⇒ 指数関数
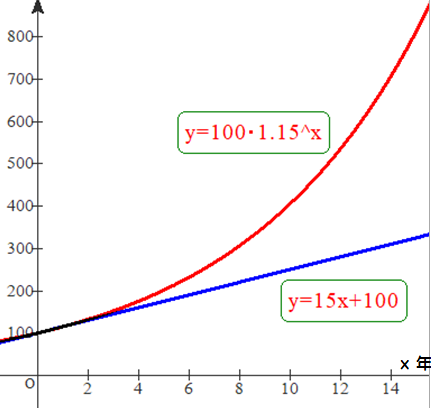
■ 1次関数と指数関数との違いに注目です.返済額についてですが,当初はともかく,時間が過ぎるにつれ”利息が利息を生む”仕組みの複利,すなわち指数関数値が,単利の1次関数値を圧倒します.ちなみに10年後の返済額は,単利:250万円,複利:約406万円となります.
■ なお,世の貸借はすべて複利計算です.この素朴かつ重要な事実を知らない成人(18歳以上とか!)が少なからずいるのでは?想像するだけで空恐ろしい!
⇒ 金銭教育は,家庭・学校教育の盲点になっていませんか?卒業時に集会等でのにわか注意喚起ではダメです.教科指導(社会,家庭,数学等)に組み込むことが肝要かと.
極低利では,単利も複利も同じ!
■ 銀行の定期預金利率は,0.002%,つまり,0.00002 程度が多く,普通預金ともなるとその1/2です.⇒ ゼロ金利政策
次の図は,計算サイト(ke!san カシオ)により,金利0.00002で10年間預金した場合の受取額を求める様子です.1.00002の10乗を瞬間的に計算します.
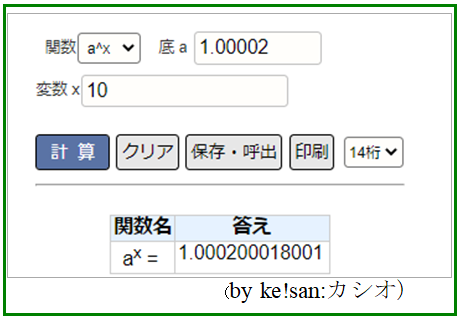
■ 仮に利率を0.002%として,100万円を定期預金します.1年後の利子は100万×0.00002=20円 で,受取額は1000020円となります.
10年後の受取額は(当然,複利),1000200.018001円で,約1000200円 です(ke!sanはすぐれもの).つまり,10年間も預けておいてタッタ200円分頂戴するワケです.
■ ここで気付くことは,端数を除く利子分200円は,単利利子分20円の10倍です.
つまり,極低利率の場合,複利計算値≓単利計算値 となりそうですね.前者は累乗計算,後者は単純かけ算ですから,計算量がまったく違うにもかかわらずです.その差は 7⁸と7×8 で実感できますね.
なぜ 複利計算値≓単利計算値 か
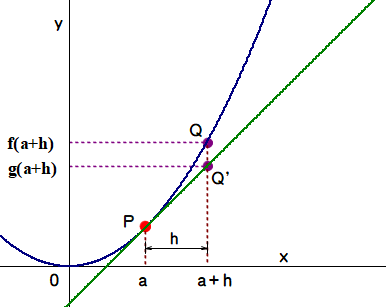
■ 図で,青線は任意の関数:y=f(x) ,緑線は曲線上の点Pにおける接線:y=g(x) です.
直感的に,hが極めて小さいとき,f(a+h)≓g(a+h) が成り立つことが分かりますね.

<補足>
■ 近似値・近似式のベースは微分です.任意の曲線の微小な変化(変位)を,接線つまり1次関数で代替するという思考です.
比例(小6)→比例の式(中1)→1次関数(中2)→変化の割合(中3)→微分(高2)→近似値(高3) こういう流れです.
■ 次回のテーマは「重心」(予定)です.重心も奥深いですね.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).