あみだくじ,重複しない?
昔(室町時代)からあるクラシックくじです.ここでは,①ゴールは重複しないワケ,②ゴールに合うくじの作り方 について考えてみましょう.
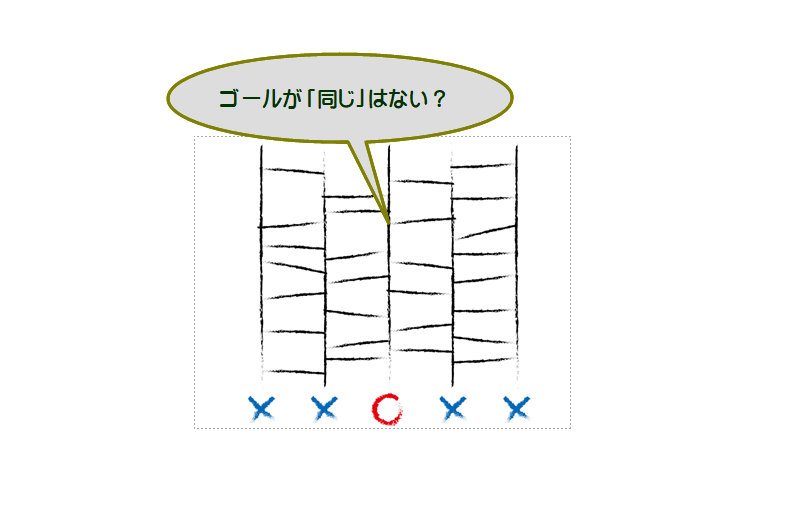
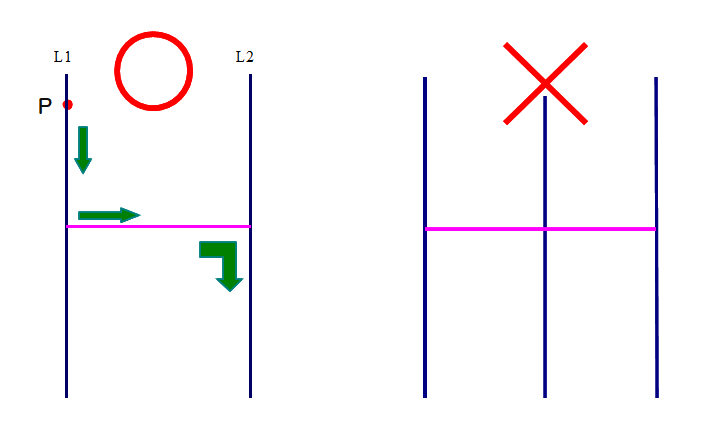
ルールを確認しておきます.縦線の上先端部に動点Pがあり,Pは次のように動きます.
①縦線を上から下に向かう(=戻らない).
②縦線L1,L2が横線mでつながっているとする.PがL1上にあるとき:Pは必ずm上を動き,L2に移動する.PがL2上にあるとき:同様にしてL1に移る.ただし,横線mでつながる縦線は2本に限る.
ゴールは重ならない
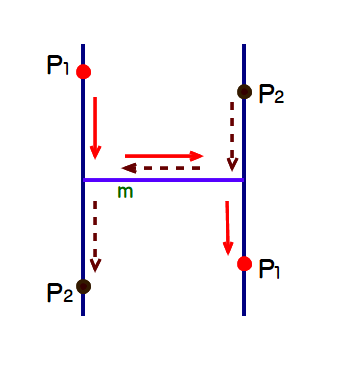
よく知られている解説から.
縦線L1, L2上のそれぞれの動点P1, P2は,横線mにより入れ換わります(互換).その際,当然ながら,動点の個数は2個で変わりません.
あみだくじは,各横線ごとの互換のくり返し(=置換)で形成されていますから,全体としての個数も不変で,n個の動点でスタートすると,ゴールもn個に分かれる,つまり,重なることはありません.
背理法による別解です.ここで背理法を用いるのは,やや大げさな気もしますが.
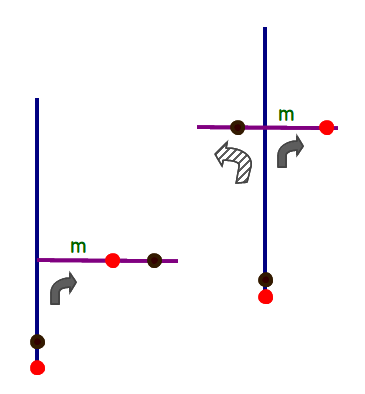
図(左)のように,別々の縦線をスタートした動点P1●, P2●が,同じゴールに着いたとします.P1,P2が通ってきたルートを逆向きにたどってみます.
直前に通過した横線mでは,ともに同じ向きからmに入って来ています(∵仮にP2が別向きから来たとすれば,図(右)のようにmは縦線と交わっていることになりますね).
さらにその前の横線でも同じことが言えます.以下,このくり返しで,最後は,動点P1, P2は同一の縦線からスタートしたことになり,これは,仮定に反します.
よって,P1, P2が重なってゴールすることはあり得ません.
ゴールからくじを作る
逆に,ゴールが与えられたとき,くじの作り方を考えましょう.
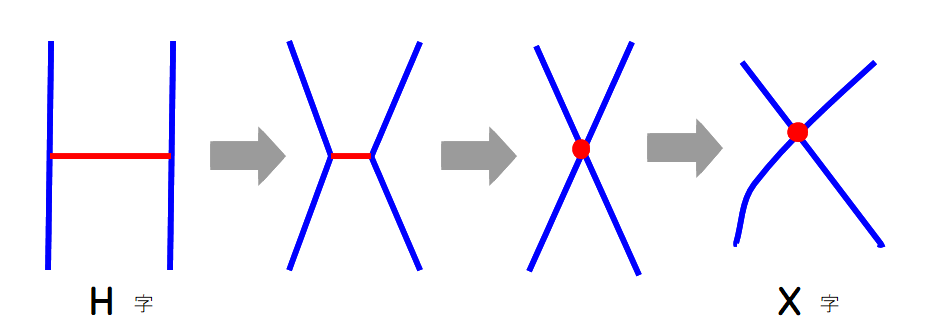
動点の入れ換え(互換)についてです.図のように,あみだくじは,H字からX字へと変化させてもその機能はそのママであり,次の3点が分かります.
①H字の横線は,横線である必要はなくX字の点でよい.⇒ ”点とは,面積をもたず,位置を示すもの”という点の定義を再認識できますね.
②縦線は,曲線(動点が戻らない限り)でもよい.
③くじ全体は,いくつかのX字を書き連ねて表すことができる.
Q1 次のような置換となるあみだくじを作りなさい.
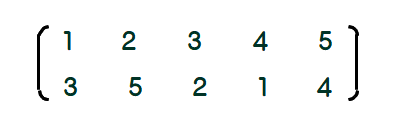
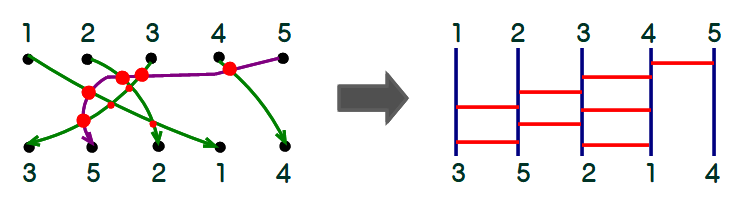
A1 下の左図のように,上下の同じ数を線で結びます.その際,3直線(曲線)以上が1点で交わらないように注意します.作図により6交点を定め,右図のように各交点と横線を対応付けるとくじが完成します.
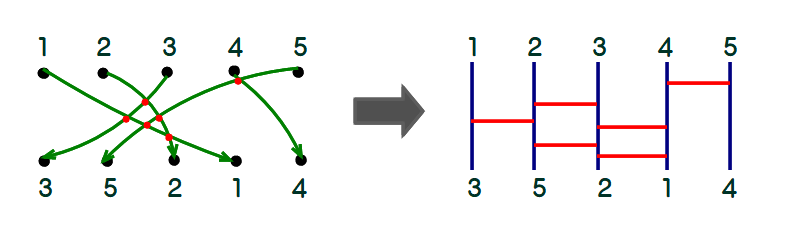
Q2 A1の別解を紹介してください.
A2 5と5を結ぶ曲線を下図のように上側を遠回りさせると,別解(の一例)になります.対応するくじは右図のとおりです.なお,同じ互換を2回続けると元に戻りますから,横線数(=交点数)の上限はなく,理論上はいくらでも増やせます.この別解の場合,A1の解と比べると,横線数は2本増えて計8本となります.
Q3 Q1の置換の場合,横線数の最小値(最適解と言います)は6であることを説明してください.
A3 下図を見てください.
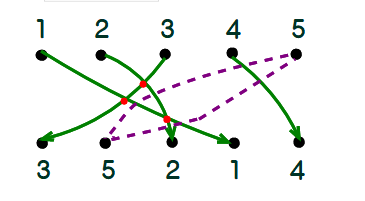
1~4まで各数ごと対応する曲線を引きます.ここまでの交点数(=横線数)は最低3個は必要ですね.
最後に5と5を結ぶ際,コースの取り方はさまざまでしょうが,少なくとも3本の曲線と交わる必要があります.
以上のことから,最適解の横線数は6本となります.
Q4 (12345)の置換の場合,最適解の最大値を求めてください.
たとえば,置換後31245の場合,横線(交点)数は最低3本必要です.しかし,Q3の最適値は6本ですので「置換後31245で,その最適値は3本」は本問の正解にはなりません.そこで,「横線数が6本より大きくなる置換はあるか?.あった場合,その最適値はいくらか」がQ4の題意です.
<補足>
■ 参考にしたあみだくじ関係の書籍等は大変多く,また,内容も広く周知されていると判断して,引用明記はしませんでした.また,最後の問Q4は,いわゆる”最小値の中の最大値”を求める問題です.
■ 次回テーマは,「素数と暗号」(予定)です.暗号と素因数分解は切り離せません.スーパーコンピューターを活かせば,素因数分解など一瞬でできるのじゃないかな?と思っていました.が,しかし・・・
■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(はじめに左, 次に右).