1°はどれくらい?
量・・・長さや重さなどいろいろあります.
その量の中で角(度)は,身近で扱う機会もほとんどなく,量感を持つのは大変です.
でも,角はサイエンスの基礎をなす,基本の基なんです.
何しろ,おそれ多くも三角関数 y=sinθ,y=cosθ,y=tanθ の変数θなのですから.

1° という角量を実感しましょう
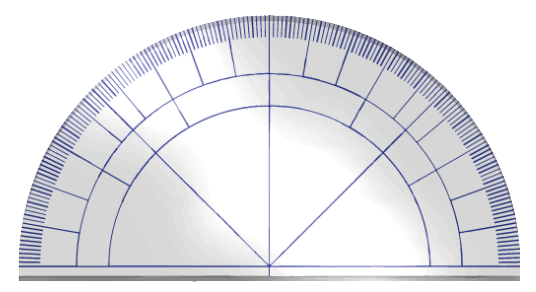
分度器を見せて,「この一目盛りが1°だよ」という解説は当然としてもそれだけで終わったら,”芸がない!”ですよね.
もう少し子供たちの生活に沿わせる工夫をして,角量認識の第一歩である量=1° に親しみを持たせましょう.
1° にこだわる理由はまだあります.それは,角と言えば,即,30°,45°,60°など,三角定規に関連する「有名角」を主に扱う風潮を憂うからです.
有名角に重きを置くわけは,テストに出題しやすい(近似値を使わずにすむ)からでしょう.
角は連続的に変化します.有名角だけがとびとび(離散的)に出現するのではありません(もちろん,1°単位で進めてもやはり離散的にはなりますが,有名角ほど極端ではない).
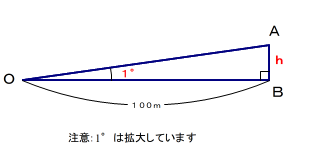
Q グランドのスタート点にいる人が,地面から1°の角で100m先にある垂直な柱を見たとき,その高さ(h)はどれほどでしょうか?
この種の問いかけに対しては,まず,「予想する」「見当を付ける」習慣を身に付けたいもの(高校生や大学生になるとかなり困難です).
なお,中学生が理解できるような説明にしましょう(→ 三角比・三角関数は使わない).
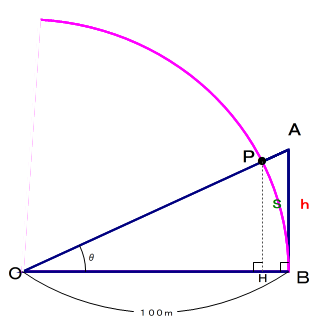
- θ:1°
- 曲線(ピンク):半径100mの円(弧)
- 点P:円と辺OAとの交点
- s:弧PBの長さ
- H:Pから辺OBへ下ろした垂線の足 とします.

つまり,角1°は,グランドのスタート点に立って,100m先にいる身長1.74m(男子高校生くらいか)の人物を見るときの仰角の大きさなのです.
補足
1 s=h と見るのはランボーじゃないか?
正しい値:100×tan1°=1.7455‥・,一方s=1.7444・・・ ですので,誤差は1mm少々.
割と”いい線行っている”と考えます.それだけ,1°という角は小さいわけです.
2 対応:θ → 弧長s について
この考え方は,高校数学で習う弧度法そのものです.つまり,中心角が弧長に比例する → 角θを弧長sと対応(代替)させる
この発想により,言い表しにくく,数式化が難しい角量の扱いが克服されました.
3 高校数学では
中心角θ,半径を1としますと,PH=sinθ, 弧長PB=θ,AB=tanθ となります.
図から分かるように,θ>0 ,θ≑0 のときは,sinθ<θ<tanθ であるとともに
かなり精度の高い近似式: sinθ≑θ≑tanθ が成り立ちます.
中学生・高校生への問い
Q 「仰角が5°の場合,100m先のゴールに立つ人の身長はどれくらいか?」という問いに対して,1.74×5(※) と計算できない理由はなぜでしょう.また,正解は,※より大きいでしょうか,小さいでしょうか?
■ 思考過程に焦点を合わせた問は,今後ますます重視されていくものと予想します.記述式かマークシート式かは別として,思考自体をねらいとして,その解説の仕方(口頭試問も増えます)まで含めての学びに注目です.
■ つまり,「思考は教室内のやり取り(アクティブラーニング)で,結果はテストで見る」のではなく,「テストで全部を見る」へ!ですね.
■ 背景には「日本の授業の改善には,まずテストを変えた方が効果的である」という発想がありそうです.
■ 何はともあれ,角については,有名角を中心とした「テストのためのテスト」対策からの脱却を図る必要があります.
<追記>
■ 次回テーマは,「”折る”操作:折り紙は深い!」(仮題)です.
折り紙は英語でもorigamiです.日本文化の一つですね.数理的な視点で教材化しましょう.
■ にほんブログ村のバナーをClickしていただければ幸いです(最初:左,次:右).