文字でつまずかせない
数学における文字対策です.何十年も前から指摘されてきたことで,広域的に改善された・効果的な指導方法が確立したといった話は耳にしておりません.何とかしようではありませんか.
指導法の前に,まず子供の気持ち(心理)のキャッチを
数年前,文字についてのアンケート調査をしました.対象は,やや数学を苦手としている,ある公立中学生徒32名(1年20名,2年12名)です.

次に,回答状況をお知らせしますが,予想をしてみてください.設問2は「結果を知るのが怖く」て,それまで実施をためらっていました.なお,設問を構成するにあたり「文字式の学習に関する研究」(前秋田大学教授杜威著,東洋館出版社)を参考にしました.

なお,学年と正解率の関係ですが,まことに残念なことに,本調査に関する限り「成長」は見られません.例:設問1で「3とa」と誤答したのは,1年3名,2年4名,「a×a×a」と誤答したのは,1年3名,2年4名,設問2(2)で「いつでもマイナス」と誤答したのは,1年13名,2年11名 といった具合.
文字指導が「かゆいところ」に届いていない?
<設問1>
■ ”3とa”:回答者7名と最多(a^3 と同数)
→ 指導者は,説明の際,3aとしては,”5本束の鉛筆3セット“などを例に挙げて話を進めています.
→ しかし,数学を苦手とする子供の多くには,その鉛筆例が届いていないのです!「今,説明したのに」と言いたいでしょうが,現実は厳しく,①聞いていない,②聞いていたとしても”効いていない”のいずれかでしょう.

→ つまり,”3a” を板書しても,イメージが浮かばず,単なるフィギュア(模様):”3とa” として映っている子供がクラスにはある程度(10%~20%?)はいます.
<設問2>
■ 知るのが「怖い」と言いましたが,予想以上でした.免許更新講習で高校籍のある受講者曰く「やらなくても結果は分かります!」.ガクッ!
■ 代数学:数の代わりに文字を用いることで数学を発展させたきた主役の一人.
しかし,たとえば「ある数をa・・・」と説明した際,aとして当初から正の数(それも自然数1,2,3程度?)しか想定できていない子供が少なからず存在するわけです.また,前述したように,aを単なるフィギュアとしてスルーする子供も加わります.次は,高校入学直後に高校生がつまずく一例です.

■ a<0 のとき,|a|=ーa について,内容をホントに理解している高校生はどのくらいいるものでしょう(勤務校だけなく広く高校生一般).私見ですが,半数未満ではないかと推測しますがいかがでしょうか.
■ 指導者に聞きますと「a=-3 などを例にして説明する」という声がほとんどです.
→ |-3|=-(-3)=3
→ しかし,数学を苦手とする少なからずの高校生(以後,苦手生という)には,その例だけでは届かないのです!「これ以上,どんな説明が?」となりますね.現実は厳しく,①ホントはすっきりしていないが,分かったことにして問題に向かう,②あきらめる のいずれかでしょう.
原因を探る
■ 設問1の結果から分かることは,例(5本束の鉛筆3セット) と 3a がリンクしておらず,ベツモノになっています..
■ 設問2で,指導者は,a=-3 などとして一般化を図ろうとします.
が,結果からは「 a=-3」は,苦手生の心には響いていないことが分かる
■ 設問1,2に共通することは,文字に対して,①イメージする力が弱い,②イメージする訓練がなされていない の2点です.
イメージ力の低下
■ スマホ全盛期時代です.映像サービスが過剰で,本来,ヒトがイメージして自分の脳細胞に焼き付けなければならないことまで,映像がサービスしてしまいます.
授業や講義でパワーポイントやスマホ画面を見て,何となく分かったつもりでそのママ終える.数学でもこういう場面が多くありませんか.
文字指導 === イメージ力の回復・アップ
a = -3 だけでは苦学生に響かない
■ なぜなら,a と -3 は,まだベツモノと映っています.=で結んだとしても,両者は苦学生の中では一体化していないのです.
■ 次のようなイメージ図が効きます!
→ この種のイメージ図は大きく(一辺50cm以上)かくこと!(一般に,数学の先生の字は小さいですね).

イメージ力アップ訓練
「a<0 のとき,|a|=ーa」(※)の解説例
■ 「これは昨日説明したことですが,まだピンときていない人,いますか?いますよね.黒板の前の方に集まってください.迷いなく分かった人は,○ページの問を解いていてください.」
■ 「これから10分間で,昔から生徒を苦しめている※を完全に克服します.いきますよ!」
■ 「aをじっくり見てください.」
「目を閉じて自分の頭の中にある黒板(頭黒板と言います)にaを大きく書いてください.はい,目を開けてください. a は小さくないですか.できるだけ大きくして.もう一度,頭の中で式全体を描いてください.」
■「 次に,aに適当な数を入れましょう.ただし,a<0という条件でしたね.△君は,どんな数を選びましたか.-2ですか.はい,○さんは? -5ね.皆さん,よろしいようですね.分数や無理数√2の人はいませんか?構いませんよ.」
■「 自分が選んだ数をaに代入した様子を頭黒板に書いてください.-3をaに代入したイメージはこんな感じになります.」

■ 「次に,|a|=ーa (※)をじっくり見てください.」
■ 「これからがヤマです.※を頭黒板に書いてください.イメージできなければ成功しません.」
■「 再度,※を書いてください.スマホはないので,自分で見えるまで頑張って!」
■ 「※の左右にあるaに自分の数を入れてください.はい,目を閉じましょう.」
■「 頭黒板で左辺と右辺をそれぞれ計算してください.どうですか?
左辺=右辺 となっていませんか? はい,目を開けて.」
■ 「△君,頭黒板の内容を黒板に書いて説明してください.」
(以下)一人一人に頭黒板の内容を口頭試問的に確認していく
■ 「最後に,質問します.右辺のー(マイナス)記号は,なぜ必要ですか?」
■ 「もう一つ.右辺(-a)全体の符号は,プラス,マイナスどっち?」
(以下略)

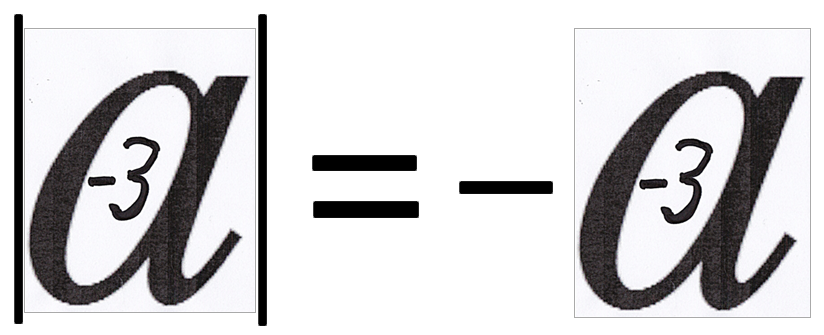
まとめ・・・です
■ 本サイト全体のテーマにもなりますが,定義や定理等の算数・数学記述を”イメージ化”できるかどうか,がポイントになります.
■ 学年が上がるにつれ,対象の”イメージ化”は難しくなります.
■ ”イメージ化”に向けて努力し続ける子供を一人でも多く育てたいものです.
※ 最近目にしたニュース見出し:”土地公示価格,県内下落幅,0.6%縮小” → グラフで表現できる子供を育てましょう!
<追記>
■ 次回テーマは,「”折る”操作:折り紙は深い!」(仮題)です.
折り紙は英語でもorigamiです.日本文化の一つですね.数理的な視点で教材化しましょう.
■ にほんブログ村のバナーをClickしていただければ幸いです(最初:左,次:右).