(-)×(-)=(+)?
■ (ー)×(ー)=(+) は,一般の大人にとっても印象に残っているようです.「そういうものだと思って覚えた」「不思議だったが理由は習ったかな?」等々の感想が多いですね.内容はさておき,数学について記憶に残っていること自体は”よいこと”かと考えます.
■ 子どもはもちろん,大人も生涯学習の視点から,この (ー)×(ー)=(+) となる(とする)理由を再確認しましょう.新発見もあるかも
※この5月にアップしましたが,気付かない間に”消滅”.多少内容をふくらませてリニューアルしました.
(-3)×(-2)=6 の解説
<教科書説明>
多少の違いはありますが,次のように,変化の様子(帰納的説明)を確認しての解説が大半です.
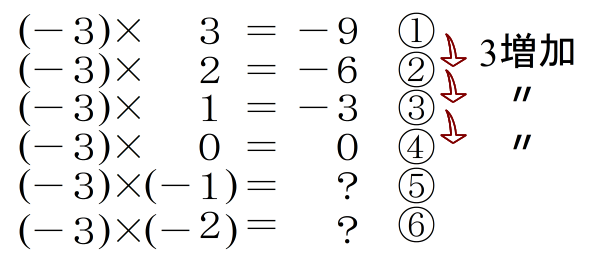
■ 右の①から②,②から③,③から④ の変化に注目してください.どれも3ずつ増加していますね.
とすると,⑤には3,⑥には6が入るのが自然であろうという説明ができます.
つまり,⑥の結果から,(-3)×(-2)=6 というワケです.
このように,特殊例から一般例を導く推論を,帰納といいます(対義語:演繹).
■ 「ルールだから」「そう習った」だけでは何とも残念!プロセスを理解した上での「ルール承認」とまいりましょう.
■ なお,マイナス×マイナス を認めないという立場も当然あり得たわけです.ただし,その時点で歩み(思考)が停止することになります.
しかし,数学に関わった人々はその立場は採らず,ルールを発展・拡張してきて今日の数学に至っています.
■ 新ルールを作る場合の「原則」があります.新ルールは「それまでのルールも含んでいるね」と確認していくと,授業にシマリが出てくるものです.本問では次の2点です.
ア:①~③のように,これまでのルール「(-)×(+)=(-)」は成り立つとする
<演繹的説明>
■ 公理(根本命令.ルールの出発点のような感じ)を基にした数の構築は専門書(「数の概念」高木貞治etc)に詳しい(白状→数ページで断念).ここでは中学生でも合点がいくように,演繹的な論理展開が少し分かるような解説をいたします.


演繹軽視の風潮
■ 過日,知り合いの指導主事氏がつぶやいた言葉が引っ掛かっています.
特に,義務段階の様子からということでしたが,数理について生活密着の意識が強いためか,帰納と類推が異様に強調され,演繹が軽視され過ぎてはいないか,という指摘でした.そう言われてみると,論理自体の持つ面白さや意義を感じさせる場面って,入試や授業でもほとんど見当たりませんね.いかがですか?
■ 不易と流行,ゆり戻しという言葉があります.かつて,数学の現代化というウエーブが日本列島を(おそらく世界も)席巻いたしました.算数・数学のすべてを集合論で説明するというようなイメージでした.集合論のココロで教材を見るのはよしとしても,末端では「集合記号の使用」で授業展開しなければならない空気が蔓延し,結局,あちこちで挫折.数年後には「廃れて」しまいました.
■ あのとき,最前線でかいた汗は,本来,別の研修・研究に費やされるべきでした.自戒を込めて言います.ミスリードした人・された人,双方の振り返りが大切かと.
その視点に立って,中学生・高校生への問題です.
Q1 ある数(a)が逆数をもつ場合,その逆数は一つしかないことを説明してください.
Q2 三平方の定理に関係した問です.
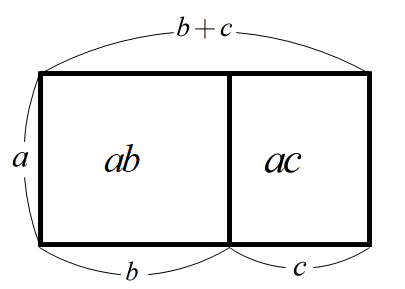
直角三角形の3辺をa,b,c(斜辺) とすると,a^2+b^2=c^2 ※が成り立ちます.
では,※が成り立つ三角形は,直角三角形になることを説明してください.
<追記>
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).


