コイン&サイコロと確率
各種保険料は,年齢や過去の発生数等を基に確率計算により決定されています.確率は統計とともに数学教育でも重視されつつあり,その存在感は強まっています(その是非は別として).
しかし,今も昔も,確率は,超苦手・大嫌いというヒトがいます.本稿では,コインとサイコロをあげ,意外性ある確率の問いかけをいたします.

どう説明します?
Q1 「サイコロをふったとき,3以上の目が出る確率は, 4/6(=2/3) と習ったけど,目は {出る,出ない} のいずれかなので,答えは1/2 ではないのですか.
Q2 正しく作られたというサイコロを24回ふりましたが,1の目が一度も出ていません.どの目も出る確率は1/6だから,平均して4回くらいは出てもよいはず.とすると,次の25回目で1の目が出ることは大いに期待できますね.
※Q1,2の解は後半
「コイン投げ」の確率は一定か

コインを10回投げて表が6回以上出る確率は,約0.377 です(※説明は下記).では,100回投げて60回以上出る確率はどうなりますか?
10:6 =100:60 より,回数が比例関係にあることから,確率も 0.377(約38%) ではないかと考えられそうですが,結論は間違い×です.しかも,答えが僅差ではなく,大きく異なる結果となります.

ところが,100回投げて60回以上出る確率は,約0.02 つまり,2% となります.38%とは,ずいぶんと開きがありますね.
<根拠となった計算式>
※以降,本稿での巨大数の扱いは,サイト 「ke!san 」(カシオ)に拠りました.強力なツールですね.深謝.

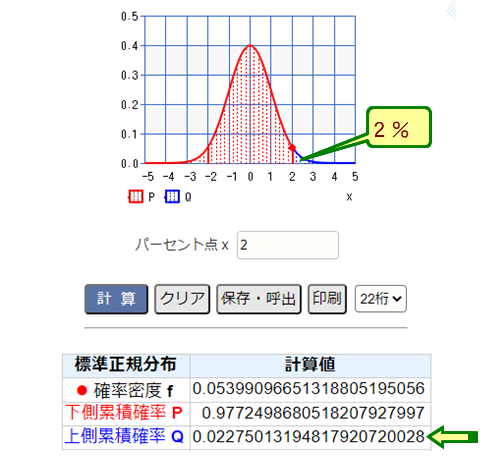
コイン投げ:38%と2% この差はどこから?
コイン投げについて,ある回数に”固定”して確率を比較してみます(←“以上”としないで).
10回投げてジャスト6回表が出る確率:P1と,100回投げてジャスト60回表が出る確率:P2について

P1=0.21 です.この値はおおよそ想像できる範囲かと.
しかし,P2≓0.01 これはどう考えますか? (70回にするとほぼ0).
コイン投げで,回数が10回のとき,表の回数は5回程度を中心に出ます.表6回も21%程度はあり得るワケです.

しかし,回数が100回ともなると,表が60回となることは,1%程度の確率となります(ちなみに,表が70回となると0%).
したがって,仮に,表が65回も出たとしたら,そのコインが不良品だった可能性が極めて大きくなります.
このように,回数(試行)が大きくなればなるほど,理論上の平均値(コインの場合は1/2×回数)に近づきます(これを大数の法則といいます).
以上,まとめますと,「コインを100回投げたとき,表が60回出ることは1%程度であり,60回以上の確率を全部寄せ集めても,2%程度にしかならない」となります.意外な結末ではないでしょうか.
<問の解説>
A1{出る,出ない}は,目の出方の場合を列挙したもの.それぞれの起こり方の確率とはベツモノになります.
コインを投げるとき,場合だけを列挙すれば,{表,裏,立つ}の3通りあります(立つ?そんな~ ⇒ 理論上ですのでok).それぞれの起こる確率は,別途定めなければなりません.「立つ」は0%でしょうが.
A2サイコロを投げる試行は,各回,互いに「独立」です.1回目に1が出たことは,2回目に影響を与えません(サイコロに記憶装置が付いていて,ある目が出る・出ないようにサイコロ自身がコントロールしておれば,「独立」ではありません).したがって,24回まで1の目が出なかったからと言って,25回目に1の目が優先されて出ることはありません.やはり,1/6の確率で出現します.
※「24回までに1の目が出ない」ことは,あり得るワケですが,メッタにないでしょうね(約1.3%).
<補足>
■ 次回テーマは,「道案内3パターン」(予定)です.小4で習いますが,xy平面座標(ガウス平面)の導入に相当します.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).