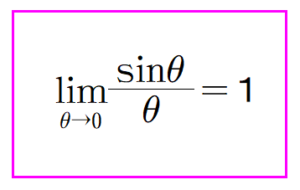わが街の犬,最小値を知っている!
以前,街中で見かけた光景です.話の展開に多少(かなり)ムリ感もありますが,お付き合いください.
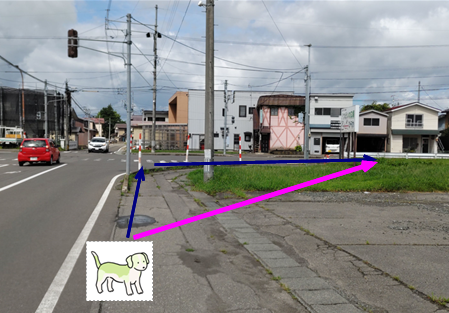
■ 図は右側角に空地がある交差点です.
迷い犬が手前から向こうへ歩いていました.
すると,彼(彼女)は,右折したかったのでしょうか,青線で示した「歩くべき歩道」など全く気にもせず,突然,ピンク色のルートを歩き出したのです!
犬の選択を数学的にみると・・・
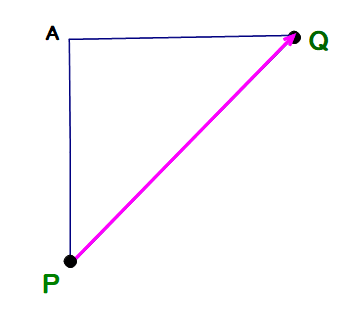
■ 点Pにいた犬は,点Qに向かうため,直線PQ上を歩いたワケです.
△APQにおいて,PA+AQ > PQ ①
が必ず成り立ちますので,数学的に,彼(犬)は最短コースPQを選んだことになります.すごいですね!← ムリ筋の解釈
※①について
三角形になるための成立条件
⇒ 三角形において2辺の和>他の1辺
⇒ PからQへ向かう道の最短距離は線分PQ
2点間距離をめぐる有名問題
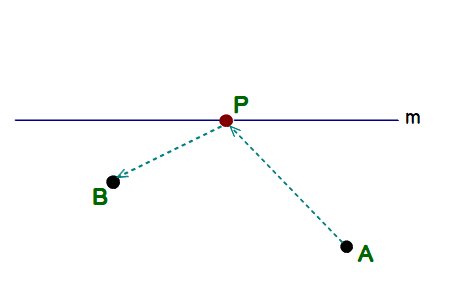
■ 次の問はご存じの方も多いことでしょう.
Q1 点Aにいる人が,川(m)で水を汲み,点Bまで歩くとする.歩く距離を最短にするには,m上で水を汲む点Pをどこにとるべきか(mは直線状とする).
A1 (略解)

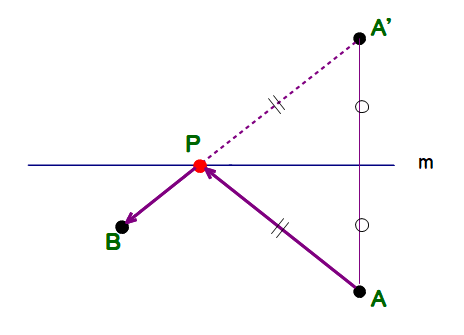
⇒ 上記以外の点をPをすると,「遠回り」になるワケですね.
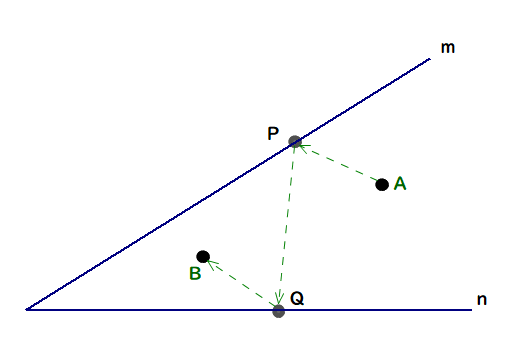
Q2 図のように,2直線m,nで囲まれた内部に点A, Bがあり,点P, Qはそれぞれm, n 上にある.線分の和:AP+PQ+QB が最小値をとるように,P, Qを定めなさい.
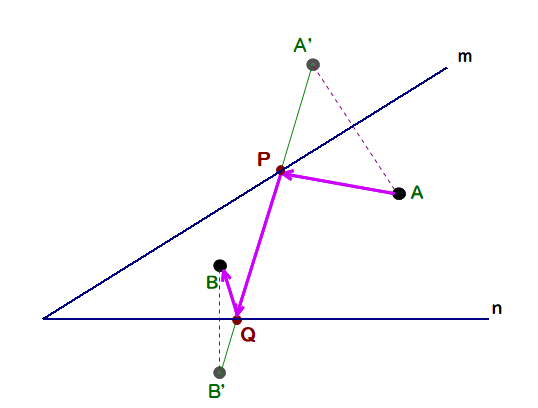
A2 (略解)
図のように,直線m, n について,点A, B の対称点をそれぞれA’,B’とする.
A’とB’を直線で結び,その直線とm,nとの交点をそれぞれP,Qとすればよい.
Q2改 座標平面上に2直線m,n
$$m:y=5x-2,n:y=\frac{1}{2}x-1 $$
と2点A(4,2),B(1,1)があります.このとき,AP+PQ+QB の最小値を求めなさい.ただし,P, Q はそれぞれ直線m,n 上の点とする.
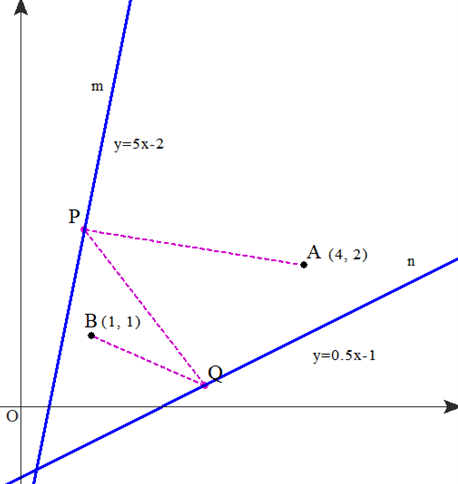
■ Q2 とほぼ同一の内容を,座標平面上の問題に設定しました.受ける印象はどうでしょうか.
座標というと即,計算に取り組むヒトも少なくありません.
その際,2点P,Qについて,$$P(a,5a-2),Q(b,\frac{1}{2}b-1)$$ とおいて,距離公式を用いると2変数の最小値問題となり,ただごとでない計算量になります. やはり,上記A2のように,対称移動する図形の問題として扱うべき例です.
三角形の成立条件の背景
■ 三角形の成立条件① についてです.
三角形の3辺をa,b,c とするとき
「a+b>c , b+c>a , c+a>b が成り立つ」ことを示しますが
ⅰ)「大げさ」な印象 ⅱ) 不等号にイコールが付かない
の2点に留意しましょう.
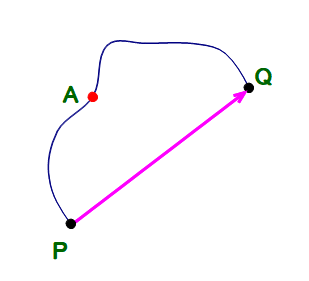
■ ⅰ)について
点PからQへ向かうとき,最短距離は直線(線分)PQであり,点Aを通る任意のコースは,遠回りになる!
という単純明快な主張であり,図形が三角形であるかどうかは本質ではありません.
⇒ 「遠回りの法則」とでも名付けたい
⇒ 三角形の成立条件:a+b>c も「遠回り」の一例であり,成り立って当たり前ですね.
■ ⅱ)について
試しにa+b=c として三角形を書いてみましょう.
<補足>
■ 次回テーマは「sinθ<θ」(予定)です.三角関数の微分を学ぶ際の必須事項の一部です.今回,取りあげた「遠回りの法則」も登場します.
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).ー