正四面体&正八面体(続き)
各種公務員試験では数的処理(大別して①判断推理、②数的推理,③資料解釈)が課せられ,その中でも「空間把握力」は判断推理問題として多くのヒトが手を焼いています.
空間把握力が公務員に必須の能力かどうかは疑問ですが,数学の教材として興味惹かれるケースもあります.次はX(twitter)上で受けた質問です(過去問かと).

■ この問をベースに本blogの前回テーマにしました(正四面体&正八面体).再度確認しましょう.↓
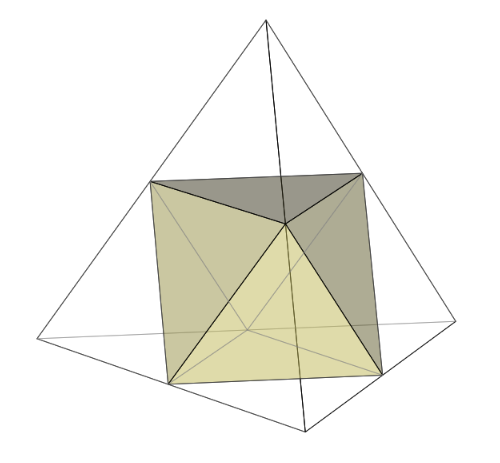
■ 正四面体の各辺の中点を結んでできる立体が正八面体(図は「Math Cal」より)
⇔ 正四面体(辺の長さ:1)4ヶを積み上げてできる正四面体(辺の長さ:2)の中空にできる立体は正八面体(下図)


■ 後半で,中空にW:正八面体ができる(入る)のイメージはいかがですか.次の図で確認してください.
逆に見ると,Wで埋めることでピンク色の土台が平らになり,その上に正四面体をチョコンと載せると1辺の長さ2の正四面体が出来上がります.

■ V₁:1辺の長さ1の正四面体,W:1辺の長さ1の正八面体とします.
ここまでをまとめると
V₂:1辺の長さ:2 の正四面体は,V₁:4ヶ,W:1ヶで形成されることがわかります.
■ 冒頭の問は,V₃:1辺の長さ:3の正四面体を形成する際,Wはいくつ必要か?という内容になります.


■ 上図を観察すると,ピンク色の箇所をV₂ の土台に置けば全体がV₃となることが分かりますね.
■ では,本題に入ります.
上記,ピンク色箇所を土台にした図を見てください.↓

(注意)ピンク土台について

■ ピンク土台だけで見ると
V₁(正四面体):7ヶ,W(正八面体):3ヶ
で構成されていますね.
したがって,V₂の分と合計してV₃の場合,W(正八面体)は4ヶです・・・(答)
Q V₃について正四面体と正八面体による詰め方(充填)は,V₁:11ヶ,W:4ヶの場合しかないことを説明してください.
<補足>
■ 上のQについてですが,(私の中で)未解決です.
■ 次回テーマは「採点がメンドーな問題をつくろう」(予定)です.難問とは限りません.
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.


