正四面体&正八面体
空間図形を鬼門とするヒトは多くいます.3次元に住んでいるヒトが,3次元の立体図形を苦手とするのはなぜでしょうか,不思議ですね.今回は,サイコロ(正六面体)に次ぐ代表的な立体図形として正四面体と正八面体に焦点を絞ります.

■ 図はCalbeeのそら豆ミーノが入っている包装ケース(試供品)で,ほぼほぼ正四面体Vです.
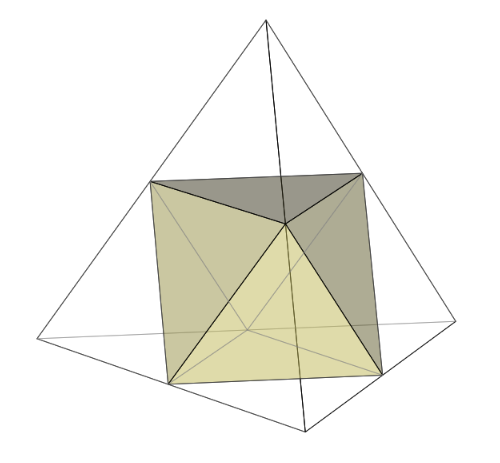
この正四面体4ヶを次の図のように重ねると,中央に空間ができますが,どんな立体になるかイメージしましょう.


■ 中央には正八面体ができます.

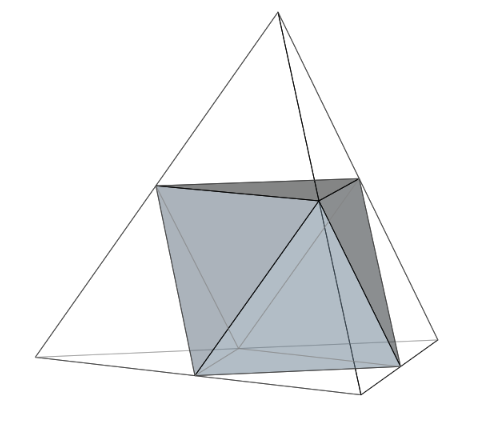
■ いかがですか.通常,正八面体と言えば,底面(正方形)が地面に置かれ上半分がピラミッドのような形を思い浮かべますが,ここでは底面が斜めになるためイメージするのに苦労するかも.(画像:Wikipedia)
視点を変えてみましょう
■ イメージするのに苦労するとき,視点を変えると一気に解決する場合もあります.
以下,辺の長さkの正四面体をVkとします.
上記Calbee包装容器による作業は
正四面体V₁ から 正四面体V₂ へ拡大したことと同じ
⇒ 逆に,V₂をV₁ へ1/2に縮小すれば正八面体が表れるはず
■ 過日,すごいサイトを見つけました
https://www.mathcal.org/canvas/soutui/0408.html (⇒ Math Cal で検索可)
■ 正四面体の各辺の中点を結ぶと正八面体ができることが一目瞭然ですね.
※上図は静止画面ですが,同サイトでは視点をマウスで動かせますので一層ナットクできます.
Q 次の問に挑戦してください.
(1)正四面体V₁ の体積を求めなさい.
(2)辺の長さ1の正八面体の体積Wを求めなさい.
A
(1) √2/12 (← 1辺の長さrの正四面体の体積:√2/12r³)
(2) まともに正面から計算を進めても正八面体の体積Wは求められますが,本問に関しては次の解法がスマートです.
正四面体Vkの体積を|Vk|とします.
V₁とV₂ は相似で,V₁:V₂=1:2 です.
したがって,|V₁|:|V₂|=1:8 ∴ |V₂|=2√2/3
全体の画像より W+4・|V₁|= |V₂| であることが分かります.
よって,W=√2/3
<補足>
■ Calbeeの包装を見て「教具」にしたくなりました(かつては牛乳パックでも四面体形がありましたね).
■ 教科書やノート,答案,さらにPC, スマホまですべて2次元表示です.ヒトは2次元の世界にあまりに浸かりすぎたため,3次元でイメージする力が削がれてしまった!と感ずる昨今です.
■ 次回テーマは「正四面体&正八面体(第2弾)」(予定)です.どういうワケか,公務員試験(上級)に空間図形がよく出題されています…公務と関係あるのでしょうか?
■ にほんブログ村ランキング(数学教育)にかかわってバナー↓のclickをお願いします(宣伝が多く恐縮です).
■ もう一つ.「ブログみる」の紹介ブログ村制作のblogを見るためのアプリです.世は正に情報過多の時代.しかし1日は24時間しかありません.できるだけ良質のブログと出会いたいものです.ブログ村が総力を傾注して立ち上げた
に関わっていきましょう.