紙面1万文字から1文字を当てる
最近は新聞が”遠く”なりましたね.
ある小学2年生クラスで「明日,授業で使うから,おうちから新聞紙1枚持ってきて」と話したところ,aさん「センセ,新聞紙ってなぁ~に?」!
この寒空光景はさておき,1紙面に約10000字は印刷できそうです(画像,宣伝等なしで).
Q1 紙面上,相手が任意に決めた1文字を当てたいときの最小質問回数を求めてください.ただし,1問に対して相手は{yes, no}で答える というルールにしたがうとします.

まず基本姿勢の確認から
■ この種の問いや疑問に対しては,おおよその見当を付けるという習慣付けが大切.
⇒ 題意理解と量概念形成のための一歩であり,また,首尾良く結果が正しく得られたときのカンドー源にもなります.
■ どんな回数が出そうですか? 確かに9999回質問すれば確実ですが,1000回とか500回という声もありそうですね.
後述しますが,14回で十分です.
■ この量概念形成のための習慣付けは,経験則から言えば,高校生では遅すぎです.学び方自体ですので理屈やセットクで身に付くほど甘くはありません.
要は,イメージする力に価値を置くかどうか,です.
⇒ 私見:イメージ力 > 計算力
■ 別場面ですが,高校の授業から
「例題:3辺の長さの比が,7:5:3 の三角形があり…」
⇒ 三角形を書かせると, 手が止まってしまう,or 鋭角三角形を描くヒトが続出
⇒ これらは,出だしの躓き! リレー1走から2走でバトンを落とすようなもので,この後の展開は至難の連続
イメージレッスンが決定的に不足しています.
{yes, no} ⇒ 二分法
■ ヒトは物事を大きく二分して処理することがよくあります.
{ 白か黒か }{ 0か1か }{ 丁か半か }といった2値化ですね.
ここでは{yes, no}として,冒頭のQ1を考えましょう.

A1 適当に直線①で紙面を二分します.
・「その文字●は①の左側にありますか?」
yes だったとして
左紙面をさらに直線②で上下に二分します.
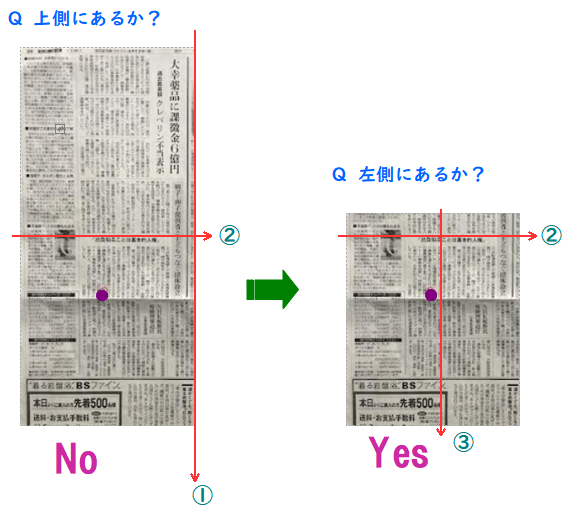
・「その文字●は②の上側にありますか?」
no だったとして
下紙面を直線③で左右二分します.
以下,同様の操作を続けていけば必ず文字●にたどり着きます.後述するように,巧くいけば13回で,14回なら確実.
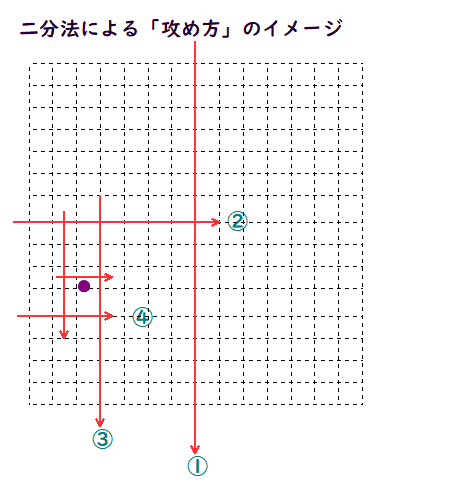
■ 直線①で二分するごとに,対象は2groupに分けられます.直線②を引くことで,4(=2²) group,さらに,直線③を引くことで,8(=2³)group ・・・と続きますね.
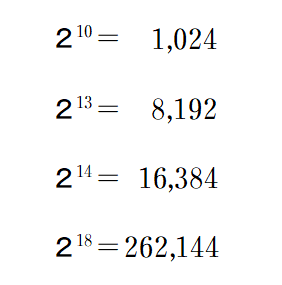
■ 表より,14回二分すれば,総数16384>10000 で,確実に文字特定できますね.

■ ある本の総文字数は
1page ⇒ 35行×30文字/行=1050文字
∴ 240page ⇒ 252000文字 です.
図のように,本の厚みを二分するpageで次々と操作を続けていけば,いつか●ページにたどり着き,計18回で文字を特定できます.
Q2 上記の本について,もし3値化:{0,1,2}で操作した場合,何回で文字特定できますか? 答は<補足>で.
<補足>
■ 累乗を扱っていると巨大数の大きさが実感できます.補正予算5兆円等々のニュースがアッサリと飛び交っています.とんでもない数値なんですが…
■ Q2の答:12回
■ 次回テーマは「数学は物理を見習うべし」(予定)です.”水槽の穴から出る水の量は一定とする” などという注釈をよく書けますね!
■ にほんブログ村のランキング(数学教育)にかかわって,バナー↓をclickしていだだければ幸いです.