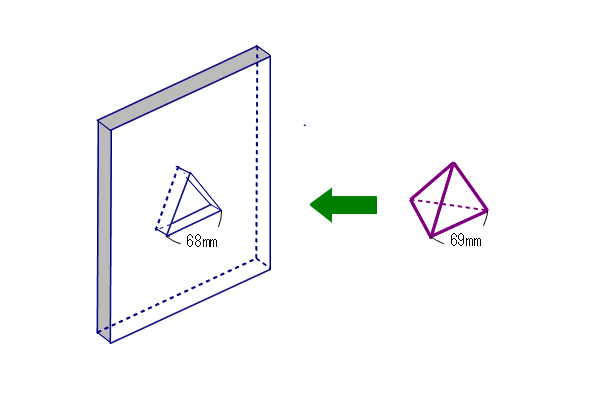
正四面体が(ちょっと小さい)正三角形の壁穴を通過する!
サイズ的にはムリなのに四面体が通過できる不思議な現象.10数年前「数学セミナー」でとり挙げられました.証明もさることながら,不思議感を味わいたく,ケッコウ精密な教具を作成しました(動画付).

証明の概略
■ 数学セミナーによる解説を基に,補足を加えながら論を進めます.
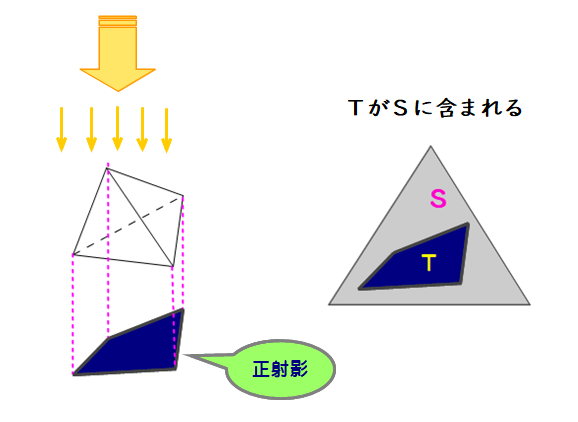
正三角形の壁穴をS,正四面体に平行光線を照射したときにできる影(正射影)をTとします.
このとき
正四面体が正三角形を通過できる ⇔ TがSに含まれる
が成り立ちますね.
■ 壁穴が正三角形ですから正四面体の正射影も三角形となるようにします.

■ 正四面体の1辺の長さを1とします.
正射影を写す平面にxy軸を導入しましょう.
⇒ 正四面体を1辺の長さ1/√2の立方体の中に埋め込む(内接させる)ことを考えます(左図).
この正四面体のセッティングが,証明の第一歩で,かなり高いハードルです.
※ 普段から立体をただ眺めていてもダメ.立体図形の中に他の図形を発見しようとするなど,観察力アップに努めたいもの.
xy座標平面への正射影
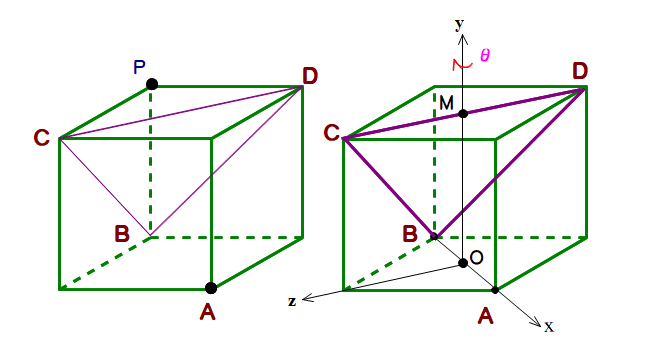
■ 左図で,たとえば四面体PBCDは正四面体ではありません(△BCDは1辺1の正三角形ですが,PB=PC=PD=1/√2 ですので).四面体ABCDは1辺が1の正四面体Uとなります(なかなか見えないかも.方眼紙上に置いた正四面体の写真画像で再度見比べてください ↓).
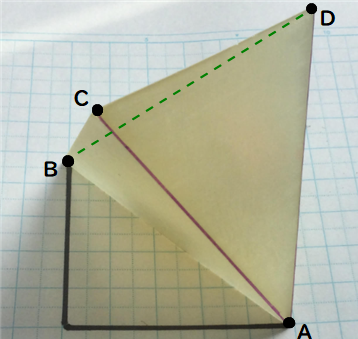
■ 上右図で,点M, O はそれぞれ辺CD, ABの中点とし,x,y,z軸を図のようにセットします.
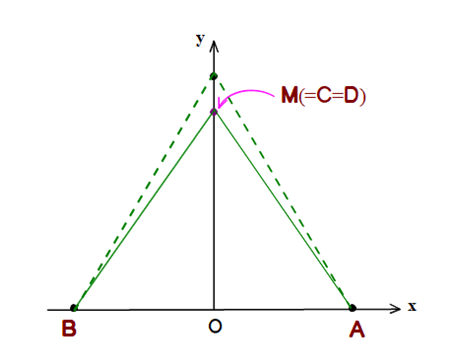
■ 図は四面体Uのxy平面への正射影Tですが,OM=1/√2 , AB=1 であり,AM=BMの2等辺三角形となりますね.
比較のため破線で1辺1の正三角形Sを描いています.TはギリギリSに含まれていますが,点A,Bが四面体と三角形上の共通点になります.
実際に四面体Uを動かそうとすると共通点辺りの摩擦によりスムーズに通過できません.
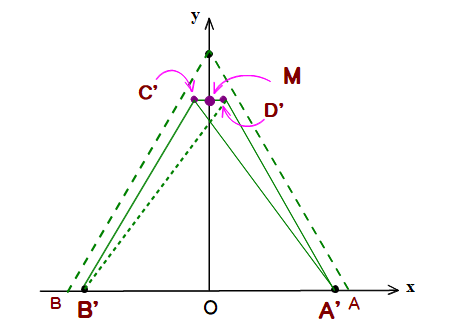
■ 摩擦をなくすにはどうすれば?
⇒ A′B′<1 とすればよいですね.
⇒ そのため,MO(y軸)を中心に,四面体Uをほんの少し回転(=θ回転)させる.かつ,Uをほんの少し上方(y軸方向)に浮かせてやるように操作すれば,全体として,正射影Tは 壁穴Sに完全に含まれることになり,四面体Uは,正三角形S内をスムーズに通過できることになります.
$※ このとき正射影Tは,四角形A’D’C’B’(等脚台形)$
$になっています.$
■ 四面体がギクシャクしながらも壁穴を通過する様子を動画で確認してみてください.↓
ナットク感を醸成できる教具
■ 本問については,初見以来,実際に手にとってナルホド感を味わいたいものと願っていました.
まず,ボール紙等厚紙は材料として不適です.なぜなら,正三角形の壁穴が,押される四面体の圧力に負け穴が広がってしまうからです.また,発泡スチロールは細工しやすいが,材質が脆く,さらに不適で問題外です.
いろいろ経緯がありまして,最後に辿り着いたのが,当時ではハイレベルの光造形方式3Dプリンターを用いての教具製作でした.3DCADの専門家である内田富士夫さん(秋田県産業技術センター)に依頼したものです.深謝・深謝です.
<補足>
■ 次回テーマは「魚か釣り竿か」です(予定).
■ にほんブログ村のランキング(数学教育)にかかわって,バナーをclickしていだだければ幸いです.↓