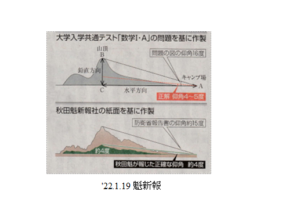
スケートの刃に同情 ⇒ その衝撃!
北京冬期五輪が始まりましたが,アイススケートの刃に”同情”します.もの凄い力が,あの細い刃にかかっているのでは?と想像するからです.
いろいろな視点から考えてみましょう(知り合いの”物理プロ”G氏に協力をあおぎました).

着地(氷)のとき,受ける衝撃とは
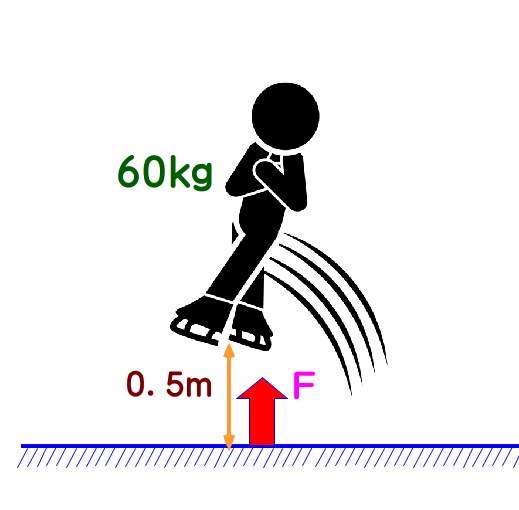
■ 体重60kgの選手が,0.5m跳び上がって,着氷したときの衝撃力Fはどれくらいでしょう?
実際は,斜めにジャンプするのですが,話を簡単にするため,垂直方向とします.

聞き慣れないことば:力積
■ 着地までの時間(0.32秒), その時の速さ(3.1m/sec) は,分かりました.
さて,衝撃の度合い(F:衝撃力)はどうなりますか?
明らかに 質量m が大きいほど,また, 速さv が大きいほどFは激しくなります.
そこで,運動する物体の激しさを示すバロメータとして,この両者の積:mv を用いることは妥当ですね.物理の世界では,mv を運動量と命名しています.
■ すると,F=mv としたくなりますが,ちょっと待ってください.決定的な要素が抜けています.
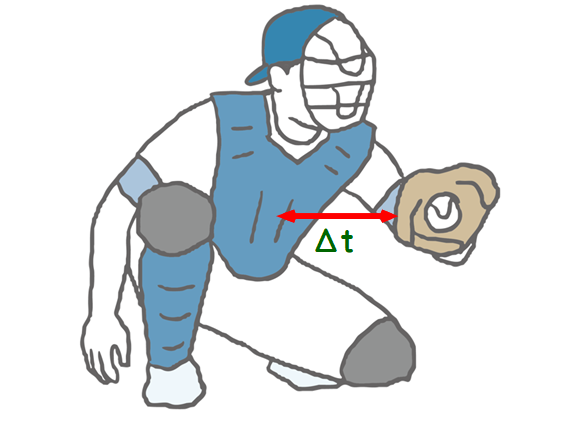
160km/h の剛速球を受けるキャッチャーを想定しましょう.
①キャッチャーが腕を伸ばしたまま,その状態でミットで球を受けたとします.
つまり,腕を棒状態にして,突っぱねたママに球を受けるワケですが,場合によっては腕が「破壊」されるでしょう.Fの値はかなり大きいと判断できます.
→ かなり以前,高校時代に野球部選手だったという20代のヒトの球を受けたことがあります.おそらく100km/h 少々の速さだったと思いますが,キャッチできず,セミプロと素人の違いを再認識しました.
②腕を伸ばして球を受ける,その瞬間,同時に腕を引き始める.球をソフトに受けながら胸元近くで球を静止させて捕球します.この場合,Fの値は①より当然小さくなりますね.
■ ①と②の違いはどこにありますか?
⇒ 球が静止するまでの時間(=Δt)に差があります.
①・・・球を受け,直ちに静止させるので(実際は,ミットの厚さもあるが),Δt≓0
②・・・Δt>0 ただし,極短時間なので,0に近い値
■ スケートの例に戻ります.
着氷によって,氷面からの力:Fを時間Δt かかって静止する ⇒ v=0 ∴ 運動量=0
そのとき,Fが一定であると仮定すると,運動量mv が F×Δt に置き換わったと考えられます.
つまり,FΔt=mv この左辺(F・Δt)を力積といいます.
F=mv÷Δt ですから,Fを小さくするには,Δt を大きくすればよいワケです.
衝撃力Fの大きさ

■ 例:m=60kg, h=0.5m のとき,v=3.1m/sec でした.仮に,Δt=0.05秒 とすると,
F=mv÷Δt
=60×3.1/0.05=3720N≓380kgw
⇒ 体重60kgの約6倍の衝撃力が生じているワケです.
■ フィギュアスケートの刃ですが,Δt という極短時間内で,体重の5~8倍程度の力を,刃先部分中心に,スケートを滑らせながら受けとめるとともに,可動域である足首や膝,腰の関節を柔らかくしてFの衝撃を緩和しているのでしょう.
佐野稔氏(元フィギュアスケート選手)は,「衝撃を和らげるためには刃の爪先で氷を割りながら,足首も使って降りる必要がある.刃全体で着氷すると『衝撃が頭まで響く』」と語っています(’18.2.7読売オンライン).
実は・・・本末転倒でした
■ 衝撃を緩和する時間:Δt の測定はかなり難しいものと考えます.
実際に, 質量あるモノ(球やスケーター)と最初に接するモノは,ミットや氷面となります.ミットは皮製であり弾力があります.氷も硬いとは言え刃先でえぐられます.
その他,ヒトの関節(手首・肘.足首等々)による緩和作用を総合してΔtを求めるワケですが,その測定方法は容易ではないと推測します.
■ ちなみに,先述したスケートの例で,Δt=0.05 と仮定しましたが,この根拠は,佐野氏のコメントの中に「現役時代,靴底に靴圧を測る装置を使用したところ,衝撃が体重の5~6倍になった」という記述がありました.
そこで,F=60kg×6=360kg として,Δt=0.05 を逆算して求めました.正に,本末転倒の論理になった次第です.
■ なお,受けるモノが氷やグローブなどではなく,完全弾性衝突のカチカチ素材でできているとすれば,F=mv/Δt で,Δt→ 0 ですから,理論上は,F→ ∞となります.
<補足>
■ スピードスケーターの刃については,コーナーでは遠心力が加わり,一段と込み入った理論となりますので,今回はパスしました.
■ 次回は,「整数方程式」(予定)です.「問題が解けりゃいいだろう」とはしたくありませんね.
■ 「にほんブログ村」のバナーをclickしていだだければ幸いです(はじめに左, 次に右).