内積って何だ?
内積については,ひたすら問題解きのための重要ツールとして扱っているヒトが少なからずいるのでは? ナットク感もナルホド感もないとすれば,モッタイナイ話.
まず 内積とは
■ 内積の定義は次のようです.
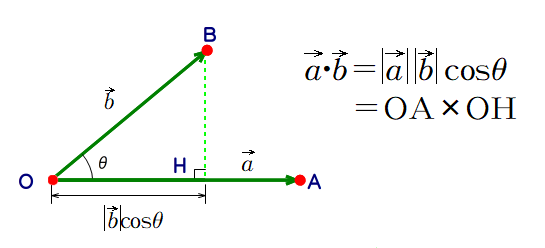
■ 「・」を普通のかけ算と混同(同一視)して,雑に書いたり,中には省略してしまう解答も見受けますが,答案の採点について言えば,極めてよろしくない印象を与えますね.「このヒトは数学のソモソモが分かっていない」⇒ その後は「厳しい目」で答案採点が続くことになるかと.
cosθ が入っているワケ
■ 物理学における仕事(W)とは
W=F× s (F:力,s:移動距離) ① のこと
日常用語の仕事とかなり違い,まぁベツモノです.
したがって,あるロッカーを力一杯押しても動かなければ,s=0,つまり,W=0 です.仕事としては評価されません.汗をかきかき押す姿など見てくれないのですね.
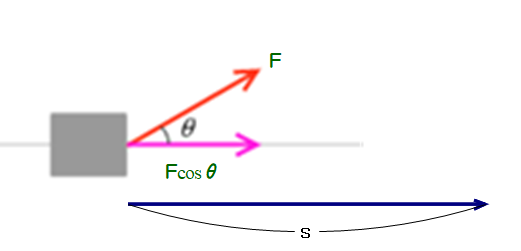
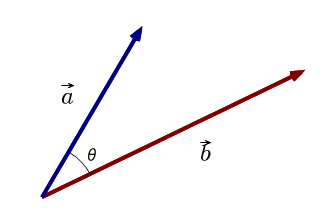
■ ①で,物体が動く向きと力の向きが一致しない,たとえば,力の向きが斜めになっている場合はどうなるでしょう.
■ 図で,力Fの水平方向の力の大きさは,Fcosθ ですね.
したがって,仕事(W)=Fcosθ×s
となり,冒頭の内積(=OH×OA)が出てきました.
■ このように,
ベクトルの内積=(物理でいう)仕事
ということが示されました.
■ したがって,内積はベクトルではなく,仕事量を表す単なる実数です.ただ,θ:鈍角 のときは,cosθ<0 ですので,内積がマイナスとなります.仕事量<0 とは理解に苦しみますが,数学の自由性と考えてください.
図形の証明と内積
■ 入試で内積に絡む問では,「内積=0」がpointですね.
内積=0 となるのは,0ベクトルを除けば,θ=90° ,つまり,ベクトル同士が直交しているときなのです.
例:直径の円周角は90°であることを証明しなさい(中3).
⇒ 教科書では,円周角=中心角÷2 を示して解説を展開しています.ここでは”90°”に注目して,内積を用いて証明しましょう.
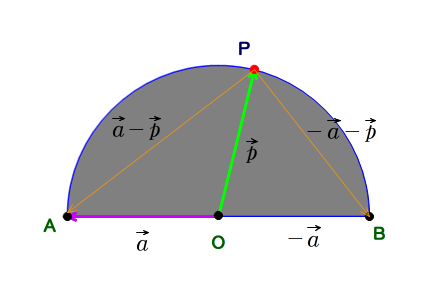

■ このほか,中線定理(ハップスの定理)も,幾何特有の「ひらめき」が不要で,もっぱら機械的な内積計算で証明が完成します.
類似度 ⇒ 今,「旬」です

■ ネットでモノを注文した際,直後から「この商品を購入したヒトはこんな商品も購入しています」といった感じで.オススメ品の知らせが,即,次々と画面に届く経験ありますよね.
■ そのモノに,前もってオススメ品知らせがストックされており,それらがただ機械的に流されてくるのではありません.
■ 過日,ネットで掃除機を買いました.数多くのモノからその掃除機を特定するにいたるまで,どんな「要素」が必要だったか,振り返りました.

例{メーカー名,価格,製造年,電源(ac電源か充電式),重さ,性能(w数),購入者評価・・・}
■ これらは,数値化可能ですね(価格・・・3段階にして,0,1,2 を充てる等).正にベクトルの各要素を示しており,上記で購入者評価までであれば,7次元のベクトルとなるワケです.
⇒ モノが ベクトル 表示される!
⇒ 3次元までなら目に見えるが,n次元(n≧4)のベクトルって存在するの?
⇒ 目には見えませんが,”存在する”として論を進めます.数学の自由性と捉えましょう.
■ データ分析をビジネスで活かす
① モノをベクトルで表し,それらのベクトル同士の類似度をフル回転させること
② クラスタリング(似たもの同士に分ける)には,類似度dataが必須
③ 類似度の理解 = cosθの理解
⇒ ほとんどの国民に知られていないところで,内積&cosθが使われているのです!


■ cos0°=1 ですから,cosθの値が1に近い(0.93など) ⇔ 2つのベクトルのなす角が0°に近い.つまり,それら2ベクトルは類似度が高い と言えます.
一般に,角θが鋭角のとき,cosθ₁<cosθ₂ ⇔ θ₁>θ₂ です.
(※)有名角の三角関数値をひたすら棒暗記する・させるような学びをしている限り,この種の論理をナットクするのは困難でしょう.
類似度について・・・参考(週刊ダイヤモンド 2018.6.30)
<補足>
■ 次回テーマは,「交点と連立方程式」(予定)です.交点と言えば,「まぁ連立方程式を解きゃいいだろう」ですが,なぜそれで交点が求まるのでしょうか?
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).


内積でcosθが入っている理由なんて考えたことありませんでした!非常に面白かったです。
hi 様
コメント,ありがとうございます.当方の思いと合致した思いです.4次元以上でも事象がベクトル表示され,さらにcosθがでかい顔して鎮座している様子は面白いですよね.充実した学生生活でありますように.