行き6km/h,帰り4km/h ⇒ 平均の速さ?
平均値が世の中を動かしています!経済指標や気象変動dataなど,平均値は日々カッポしています.この”平均”ですが,計算自体は実に単純で簡単.しかし,意外な盲点もありそうです.
戸惑う”平均計算”
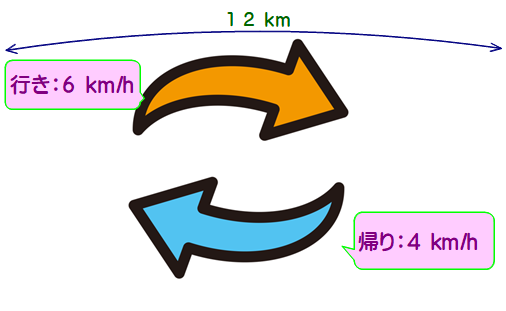
■ 12kmの道のりを,行き:6km/h, 帰り: 4km/h で往復したとき,平均の速さは?
⇒ (6+4)÷2= 5 km/h ではありません!
■ 往復距離:24 km, かかった時間:往路2h,復路3hで計5時間
⇒ 平均の速さ:24÷5= 4.8 km/h となります.
量に2タイプあり


Q1 5mと2mのヒモを結びました.全体の長さは?
Q2 20°Cと50°Cのお湯を混ぜました.全体の温度は?
A Q1は問題なしですね.
Q2で 20+50=70, よって,70°C とするヒトはいないと思いますが,温度の場合は,なぜ数を加えることができないのでしょうか?
■ 長さ・重さ・体積など,数を加えることができる量・・・外延量(extensive quantity)
速さ・温度・人口密度など,数を加えることができない量・・・内包量(implicate quantity) といいます.
⇒ 外苑量には m, g, ㍑ ,内包量には km/h, 人/km² などの単位が付きます.
参考「算数・数学なぜなぜ事典」(日本評論社)
平均の速さのナットク
■ 「速さは内包量.よって,平均の速さは,(6+4)÷2 では求められません」と言われてもスッキリしませんね.グラフによる「図解」で考えてみましょう.
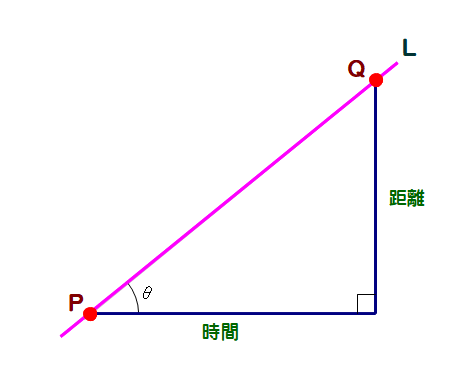
■ 速さ(v)=距離÷時間 です.
左図で,v=(直線PQの傾き) を表しています.つまり,v=tanθ です.
例:12kmを6時間で走る ⇒ v=12/6=2(km/h) ∴ tanθ=2
■ 次は,12kmを往路6km/h, 復路4km/h で往復したときのグラフです.
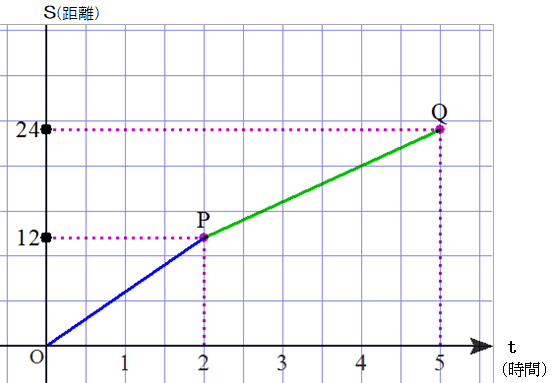
■ 往路6km/h⇔直線OPの傾き:6, 復路4km/h⇔直線PQの傾き:4 ですね.
では,往復24kmの平均の速さはどのように表せますか?
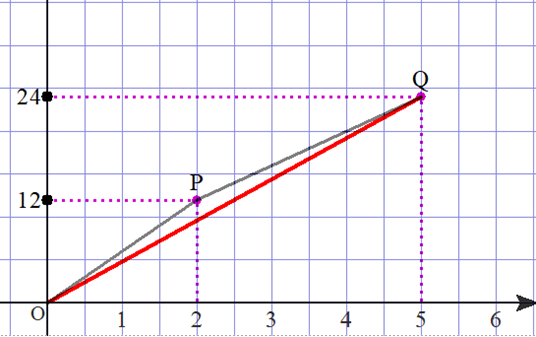
■ 図で,往復の平均の速さ=直線OQの傾き です.ここで,OQの傾き:4.8 であり,5 とはならないことが分かります.
■ もう少し違いがハッキリする例を紹介しましょう.下図で,OP間が90km/h, PQ間が10km/h とします.
どう見ても,OQの傾き < (90+10)÷2=50
⇒ PQ間がOP間より長い時間なので,PQ間の傾き:10に”引っ張られ”,平均の速さは,50よりはるかに小さい数になるワケです.
<補足>
■ 速さが直線の傾きで示されますが,その際,x軸:時間t,y軸:距離sであることが重要です.すなわち,ST座標でなければなりません.
■ 次回テーマは,「内積って何だ?」(予定)です.つかみ所のない内積ですが,「入試で頻出,よって不可欠」だけでは残念!
■ にほんブログ村のバナーをclickしていだだければ幸いです(最初:左,次:右).